Orthogonalité et distances dans l'espace
Un conseil: revoir le cours sur le produit scalaire de la classe de première!
I Produit scalaire dans l'espace
Remarque: les définitions et propriétés relatives au produit scalaire de deux vecteurs du plan s'étendent à l'espace. En voici quelques unes.
Définition
Soient ${u}↖{→}$ un vecteur, et A et B deux points tels que ${u}↖{→}={AB}↖{→}$.
La norme de ${u}↖{→}$ est la distance AB.
Ainsi: $ ∥{u}↖{→} ∥=AB$.
Voici la première formule à connaître.
Définition Produit scalaire et angle
Soient ${u}↖{→}$ et ${v}↖{→}$ deux vecteurs.
Le produit scalaire de ${u}↖{→}$ par ${v}↖{→}$, noté ${u}↖{→}.{v}↖{→}$, est le nombre réel défini de la façon suivante:
Si ${u}↖{→}={0}↖{→}$ ou si ${v}↖{→}={0}↖{→}$, alors ${u}↖{→}.{v}↖{→}=0$
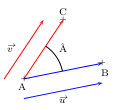
Sinon, si A, B et C sont trois points tels que ${u}↖{→}={AB}↖{→}$ et ${v}↖{→}={AC}↖{→}$,
alors: ${u}↖{→}.{v}↖{→}=∥{u}↖{→} ∥×∥{v}↖{→} ∥×\cos {A}↖{⋏}\,\,\,\,$
Cette dernière égalité s'écrit alors: $${AB}↖{→}.{AC}↖{→}=AB×AC×\cos {A}↖{⋏}\,\,\,\,$$
Norme et produit scalaire
Soient ${u}↖{→}$ un vecteur. On a alors: $$ ∥{u}↖{→} ∥^2={u}↖{→}.{u}↖{→}\,\,\,\,\,$$.
Propriétés
Soit ${u}↖{→}$, ${v}↖{→}$ et ${w}↖{→}$ trois vecteurs et $λ$ un réel.
Propriété de symétrie: ${u}↖{→}.{v}↖{→}={v}↖{→}.{u}↖{→}$
Propriétés de linéarité: $(λ{u}↖{→}).{v}↖{→}=λ×({u}↖{→}.{v}↖{→})$
${u}↖{→}.({v}↖{→}+{w}↖{→})={u}↖{→}.{v}↖{→}+{u}↖{→}.{w}↖{→}$
Voici le second type de formule à connaître.
Propriété Produit scalaire et projeté orthogonal
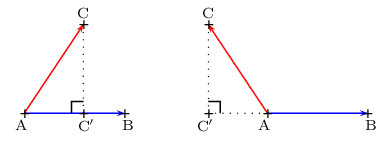
Si A et B sont deux points distincts,
Si C' est le projeté orthogonal de C sur (AB),
alors:
$${AB}↖{→}.{AC}↖{→}=AB×AC'\,\,\,$$ si ${AB}↖{→}$ et ${AC'}↖{→}$ ont même sens.
$${AB}↖{→}.{AC}↖{→}=-AB×AC'\,\,\,$$ si ${AB}↖{→}$ et ${AC'}↖{→}$ sont de sens opposés.
$${AB}↖{→}.{AC}↖{→}=0\,\,\,$$ si ${AC'}↖{→}={0}↖{→}$.
Voici le troisième type de formule à connaître.
Propriété Produit scalaire et normes
Soient ${u}↖{→}$ et ${v}↖{→}$ deux vecteurs.
Voici les 3 identités de polarisation.
${u}↖{→}.{v}↖{→}={1}/{2}\({∥{u}↖{→}∥}^2+{∥{v}↖{→}∥}^2-{∥{u}↖{→}-{v}↖{→}∥}^2\)\,\,\,\,\,\,\,\,$
${u}↖{→}.{v}↖{→}={1}/{4}\({{∥{u}↖{→}+{v}↖{→}∥}^2-{∥{u}↖{→}-{v}↖{→}∥}^2\)\,\,\,\,\,\,\,\,$
Et en voici deux applications concrètes.
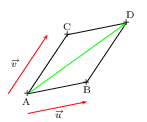
Si ABDC est un parallélogramme tel que ${u}↖{→}={AB}↖{→}$ et ${v}↖{→}={AC}↖{→}$,
alors la première identité devient:
$${AB}↖{→}.{AC}↖{→}={1}/{2}(AD^2-AB^2-AC^2)\,\,\,\,\,$$
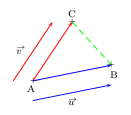
Si A, B et C sont trois points tels que ${u}↖{→}={AB}↖{→}$ et ${v}↖{→}={AC}↖{→}$,
alors la seconde identité devient:
alors: $${AB}↖{→}.{AC}↖{→}={1}/{2}(AB^2+AC^2-BC^2)\,\,\,\,\,$$.
La première identité de polarisation permet de retrouver les autres. Mais mieux vaut les savoir toutes pour être plus efficace!
Exemple
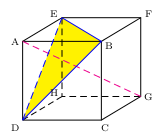
ABCDEFGH est un cube de côté $a$ (non nul) dessiné ci-contre.
I est le milieu de [BC].
On admet que EBI est rectangle en B.
1. Calculer les distances ED, DI et EI en fonction de $a$.
2. Exprimer le produit scalaire ${DI}↖{→}.{DE}↖{→}$ en fonction de $a$.
3. Déterminer une mesure, arrondie au dixième de degré,
de l'angle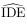 
.
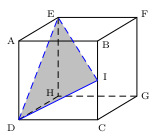
4. Soit E' le pied de la hauteur issue de E du triangle EID.
Calculer la distance DE' en fonction de $a$.
Placer le point E' sur le graphique.
Corrigé
1. Comme I est le milieu de [BC], on a : $CI={a}/{2}$. Cela servira dans les calculs...
Dans le cube ABCDEFGH, il est clair que le triangle EDA est rectangle en A.
D'où: $ED^2=EA^2+AD^2=a^2+a^2=2a^2$, et donc: $ED=√{2}a$.
Notons pour la suite que $EB^2=ED^2=2a^2$.
Comme ci-dessus, on note que DCI est rectangle en C,
et par là: $DI^2=DC^2+CI^2=a^2+({a}/{2})^2={5}/{4}a^2$, et donc: $DI={√{5}}/{2}a$.
Enfin EBI est rectangle en B.
D'où: $EI^2=EB^2+BI^2=2a^2+({a}/{2})^2={9}/{4}a^2$, et donc: $EI={3}/{2}a$.
2. Comme l'énoncé ne cite que des distances, il est tentant d'appliquer une identité de polarisation.
Utilisons la formule: $${u}↖{→}.{v}↖{→}={1}/{2}\({∥{u}↖{→}∥}^2+{∥{v}↖{→}∥}^2-{∥{u}↖{→}-{v}↖{→}∥}^2\)\,\,\,\,\,\,\,\,$$
${DI}↖{→}.{DE}↖{→}={1}/{2}(DI^2+DE^2-EI^2)={1}/{2}({5}/{4}a^2+2a^2-{9}/{4}a^2)$
Soit: ${DI}↖{→}.{DE}↖{→}={1}/{2}a^2$.
Autre méthode: utilisons la formule: $${u}↖{→}.{v}↖{→}={1}/{2}\({∥{u}↖{→}+{v}↖{→}∥}^2-{∥{u}↖{→}∥}^2-{∥{v}↖{→}∥}^2\)\,\,\,\,\,\,\,\,$$
${ID}↖{→}.{DE}↖{→}={1}/{2}(IE^2-ID^2-DE^2)={1}/{2}({9}/{4}a^2-{5}/{4}a^2-2a^2)$
Soit: ${ID}↖{→}.{DE}↖{→}=-{1}/{2}a^2$.
Et donc: ${DI}↖{→}.{DE}↖{→}={1}/{2}a^2$. (Attention au changement de signe; ${DI}↖{→}.{DE}↖{→}=-{ID}↖{→}.{DE}↖{→}$)
3. Comme il est question d'un angle, il est tentant d'appliquer la définition du produit scalaire.
On a: ${DI}↖{→}.{DE}↖{→}=DI×DE×\cos {D}↖{⋏}$.
Soit: ${1}/{2}a^2={√{5}}/{2}a×√{2}a×\cos {D}↖{⋏}$.
Et en simplifiant par $a$ (non nul), on obtient: ${1}/{√{10}}=\cos {D}↖{⋏}$.
Soit: $\cos {D}↖{⋏}≈0,3162$. Et par là:
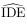$≈71,6°$.
4. Comme l'énoncé évoque une hauteur, il est tentant d'appliquer la formule relative aux projetés orthogonaux.
Le point E', pied de la hauteur issue de E du triangle EID, est donc le projeté orthogonal de E sur (DI).
Par conséquent, on a: ${DI}↖{→}.{DE}↖{→}={DI}↖{→}.{DE'}↖{→}$.
On notera que ${DI}↖{→}$ et ${DE'}↖{→}$ sont de même sens car l'angle 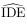est aigu (il vaut environ $71,6°$).
Par conséquent, on obtient: ${DI}↖{→}.{DE}↖{→}=DI×DE'$.
Soit: ${1}/{2}a^2={√{5}}/{2}a×DE'$.
Donc: $DE'={a}/{√{5}}$.
Pour placer le point E', il suffit d'avoir la valeur du quotient ${DE'}/{DI}$
On calcule donc: ${DE'}/{DI}={{a}/{√{5}}}/{{√{5}}/{2}a}={a}/{√{5}}×{2}/{√{5}a}$
Soit: ${DE'}/{DI}={2}/{5}$.
Cela permet de placer E' avec précision.
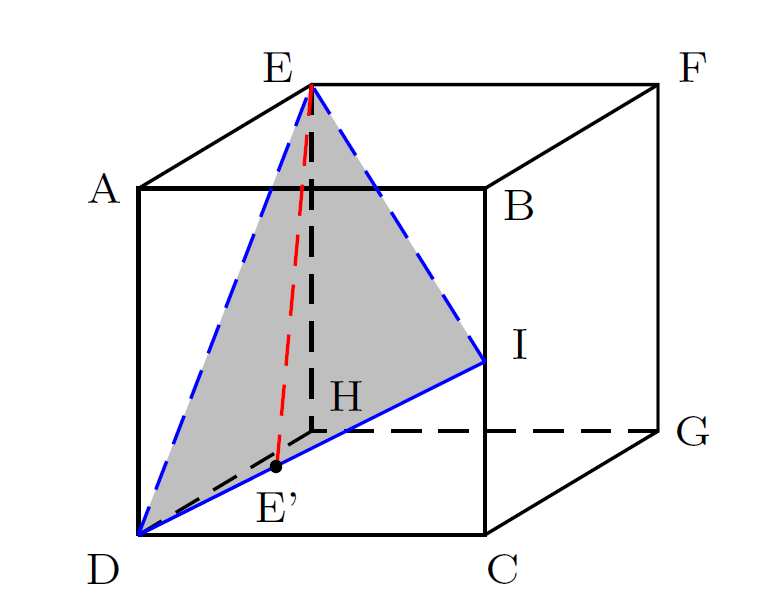
Attention! L'angle droit en E' est déformé par la perspective cavalière. Par contre, les rapports de distance sont conservés.
Définition
Deux vecteurs ${u}↖{→}$ et ${v}↖{→}$ sont orthogonaux
si et seulement si ${u}↖{→}.{v}↖{→}=0$.
Définition
Le repère $(O,{i}↖{→},{j}↖{→},{k}↖{→})$ ou la base $({i}↖{→},{j}↖{→},{k}↖{→})$ est orthonormé si et seulement si les vecteurs ${i}↖{→}$, ${j}↖{→}$ et ${k}↖{→}$ sont orthogonaux deux à deux et ont chacun pour norme 1.
Voici le quatrième type de formule à connaître.
Propriété Produit scalaire et coordonnées
L'espace est muni d'une base orthonormée $({i}↖{→},{j}↖{→},{k}↖{→})$.
Soit ${u}↖{→}(x\,;\,y\,;\,z)$ et ${v}↖{→}(x'\,;\,y'\,;\,z')$ deux vecteurs.
alors: ${u}↖{→}.{v}↖{→}=xx'+yy'+zz'$
Propriétés
L'espace est muni d'une base orthonormée $({i}↖{→},{j}↖{→},{k}↖{→})$.
Si ${u}↖{→}$ a pour coordonnées $(x\,;\,y\,;\,z)$, alors $$ ∥{u}↖{→} ∥=√{x^2+y^2+z^2}\,\,\,$$
L'espace est muni d'un repère orthonormé $O,{i}↖{→},{j}↖{→},{k}↖{→})$.
Soient $A(x_A;y_A;z_A)$ et $B(x_B;y_B;z_B)$ deux points
Alors: $$ AB=√{(xB-x_A)^2+(yB-y_A)^2+(zB-z_A)^2}\,\,\,$$
Exemple
Reprenons l'exemple précédent.
ABCDEFGH est un cube de côté $a$ (non nul).
I est le milieu de [BC].
Plaçons nous dans le repère $(D,{DC}↖{→},{DH}↖{→},{DA}↖{→})$.
Ce repère est clairement orthonormé, et nous autorise à calculer des produits scalaires.
Donner (sans justifier) les coordonnées des points D, I et E, puis déterminer une mesure,
arrondie au dixième de degré, de l'angle .
Corrigé
D( 0 ; 0 ; 0 ) I( 1 ; 0 ; 0,5 ) E( 0 ; 1 ; 1 )
On a alors : ${DI}↖{→}$( 1 ; 0 ; 0,5 ) ${DE}↖{→}$( 0 ; 1 ; 1 ).
${DI}↖{→}.{DE}↖{→}=1×0+0×1+0,5×1=0,5$
Or ${DI}↖{→}.{DE}↖{→}=DI×DE×\cos {D}↖{⋏}$.
On obtient donc $0,5=DI×DE×\cos {D}↖{⋏}$.
On calcule donc : ${DI}↖{→}.{DI}↖{→}=1^2+0^2+0,5^2=1,25$ et par là: $DI=√{1,25}$
De même: ${DE}↖{→}.{DE}↖{→}=0^2+1^2+1^2=2$ Et par là: $DE=√{2}$
Par conséquent: $0,5=√{1,25}×√{2}×\cos {D}↖{⋏}$.
Et donc: $\cos {D}↖{⋏}={0,5}/{√{1,25}×√{2}}≈0,3162$. Et par là:
$≈71,6°$.
Savoir faire
Le produit scalaire se calcule avec 4 types de formules: la première concerne distances et angles, la seconde le projeté orthogonal, la troisième les normes, et la dernière les coordonnées dans un repère orthonormé.
Il faut choisir la formule adaptée à l'exercice!
II Orthogonalité dans l'espace
a. Droites orthogonales
Définition
Soit $d$ une droite de vecteur directeur ${u}↖{→}$.
Soit $d'$ une droite de vecteur directeur ${v}↖{→}$.
$d$ et $d'$ sont orthogonales si et seulement si ${u}↖{→}.{v}↖{→}=0$.
Propriété
Soient $d$ et $d'$ deux droites orthogonales.
Si $d$ et $d'$ ne sont pas coplanaires, alors elles ne sont pas sécantes.
Si $d$ et $d'$ sont coplanaires, alors elles se coupent selon un angle droit; on dit qu'elles sont perpendiculaires.
b. Droites et plans orthogonaux
Définition et Propriété
Soit $d$ une droite de vecteur directeur ${u}↖{→}$.
Soit $\P$ un plan de vecteurs directeurs ${v}↖{→}$ et ${w}↖{→}$.
$d$ et $\P$ sont orthogonaux si et seulement si
${u}↖{→}.{v}↖{→}=0$ et ${u}↖{→}.{w}↖{→}=0$.
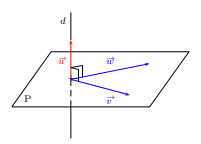
$d$ et $\P$ sont orthogonaux si et seulement si
quels que soient les points A et B de $\P$, on a: ${u}↖{→}.{AB}↖{→}=0$.
Exemple
Reprenons le cube ABCDEFGH de côté $a$ (non nul) dessiné ci-contre.
I est le milieu de [BC].
Expliquer pourquoi EBI est rectangle en B.
Corrigé
${BA}↖{→}$ et ${BF}↖{→}$ sont 2 vecteurs directeurs du plan (BAF).
La face ABCD est un carré, et donc $(BC)⊥(BA)$, et donc: ${BC}↖{→}.{BA}↖{→}=0$ .
De même, avec le carré BFGC, on obtient: $(BC)⊥(BF)$, et donc: ${BC}↖{→}.{BF}↖{→}=0$ .
${BC}↖{→}$ est donc orthogonal à 2 vecteurs directeurs du plan (BAF), et par là, ${BC}↖{→}$ est orthogonal à tout vecteur de ce plan, en particulier à ${EB}↖{→}$.
Donc les droites (BC) et (EB), sécantes en B, sont perpendiculaires.
Or, comme I est le milieu de [BC], les droites (BC) et (BI) sont confondues.
Par conséquent, (BI) est perpendiculaire à (EB).
On en déduit finalement que EBI est rectangle en B.
Définition
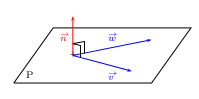
Soit ${n}↖{→}$ un vecteur non nul
Soit $\P$ un plan de vecteurs directeurs ${v}↖{→}$ et ${w}↖{→}$.
Le vecteur ${n}↖{→}$ est normal au plan $\P$
si et seulement si ${n}↖{→}.{v}↖{→}=0$ et ${n}↖{→}.{w}↖{→}=0$.
Propriété
Soit $d$ une droite de vecteur directeur ${n}↖{→}$
Soit $\P$ un plan.
$d$ et $\P$ sont orthogonaux
si et seulement si le vecteur ${n}↖{→}$ est normal au plan $\P$
Exemple
Reprenons encore une fois le cube ABCDEFGH de côté $a$ (non nul).
Partie 1.
Sans utiliser de coordonnées, montrer que la droite (AG) est orthogonale au plan (EBD).
Il est conseillé de commencer par montrer que ${EB}↖{→}$ est orthogonal à deux vecteurs directeurs du plan (AFG).
Partie 2.
Retouvons le résultat précédent à l'aide de la géométrie analytique.
Plaçons nous dans le repère $(D,{DC}↖{→},{DH}↖{→},{DA}↖{→})$.
Ce repère est clairement orthonormé, et nous autorise à calculer des produits scalaires.
Donner (sans justifier) les coordonnées des points D, A, B, G, et E, puis montrer que la droite (AG) est orthogonale au plan (EBD).
Corrigé
Partie 1.
La face ABFE du cube est un carré, et par là ${EB}↖{→}$ est orthogonal à ${AF}↖{→}$.
L'arête [FG] du cube est clairement orthogonale à la face ABFE, et par là, le vecteur ${FG}↖{→}$ est orthogonal à tout vecteur appartenant à la direction de cette face,
en particulier au vecteur ${EB}↖{→}$.
Finalement, ${EB}↖{→}$ est orthogonal à ${AF}↖{→}$ et à ${FG}↖{→}$, qui sont deux vecteurs directeurs du plan (AFG).
Donc ${EB}↖{→}$ est orthogonal à tout vecteur appartenant à la direction de (AFG), en particulier au vecteur ${AG}↖{→}$.
De même, on peut montrer que ${DB}↖{→}$ est orthogonal à tout vecteur appartenant à la direction de (ACG), en particulier au vecteur ${AG}↖{→}$.
Et finalement, ${AG}↖{→}$ est orthogonal à ${EB}↖{→}$ et à ${DB}↖{→}$, qui sont deux vecteurs directeurs du plan (EBD).
Par conséquent, la droite (GA) est orthogonale au plan (EBD).
Partie 2.
D( 0 ; 0 ; 0 ) A( 0 ; 0 ; 1 ) B( 1 ; 0 ; 1 )
G( 1 ; 1 ; 0 ) E( 0 ; 1 ; 1 )
On a alors : ${DB}↖{→}$( 1 ; 0 ; 1 ) ${DE}↖{→}$( 0 ; 1 ; 1 )
${AG}↖{→}$( 1 ; 1 ; -1 ).
Primo: ${DB}↖{→}$ et ${DE}↖{→}$, vecteurs non nuls dont les coordonnées ne sont pas proportionnellles, ne sont donc pas colinéaires,
et par là, ils forment un couple de vecteurs directeurs du plan (EBD).
Secundo: ${AG}↖{→}$ est un vecteur directeur de la droite (AG).
Tertio: ${AG}↖{→}.{DB}↖{→}=1×1+1×0+(-1)×1=0$ ${AG}↖{→}.{DE}↖{→}=1×0+1×1+(-1)×1=0$
Par conséquent, la droite (AG) est orthogonale au plan (EBD).
Propriété
Soient ${n}↖{→}$ un vecteur non nul et A un point de l'espace.
L'ensemble des points M de l'espace tels que ${AM}↖{→}.{n}↖{→}=0$ est le plan $\P$
qui passe par A et admet ${n}↖{→}$ pour vecteur normal.
c. Projetés orthogonaux
Propriété
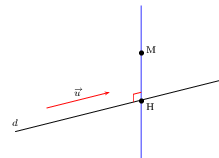
Soit M un point de l'espace.
Soit $d$ une droite de vecteur directeur ${u}↖{→}$
Le projeté orthogonal du point M sur la droite $d$ est le point H si et seulement si H appartient à $d$ et les vecteurs ${u}↖{→}$ et ${MH}↖{→}$ sont orthogonaux.
Propriété
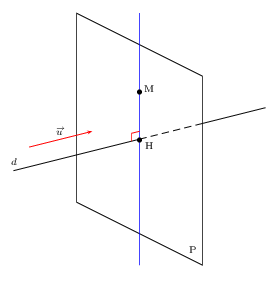
Soit M un point de l'espace.
Soit $d$ une droite de vecteur directeur ${u}↖{→}$
Le projeté orthogonal du point M sur la droite $d$ est le point H si et seulement si H appartient à $d$ et au plan P passant par M et de vecteur normal ${u}↖{→}$.
Définition
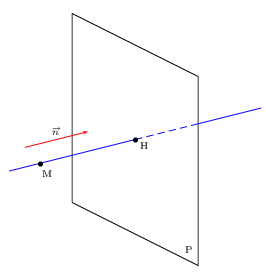
Soit M un point de l'espace.
Soit $P$ un plan de vecteur normal ${n}↖{→}$.
Le projeté orthogonal du point M sur le plan P est le point H si et seulement si H appartient à P et à la droite passant par M et de vecteur directeur ${n}↖{→}$.
Propriétés
Le projeté orthogonal d'un point M sur une droite $d$ est le point de $d$ le plus proche de M.
Le projeté orthogonal d'un point M sur un plan P est le point de P le plus proche de M.
Définitions
La distance entre un point M et une droite $d$ est la distance entre M et son projeté orthogonal sur $d$.
La distance entre un point M et un plan P est la distance entre M et son projeté orthogonal sur P.
Exemple
Reprenons encore une fois le cube ABCDEFGH de côté $a$.
Nous savons déjà que la droite (AG) est orthogonale au plan (EBD).
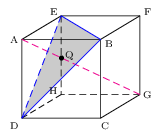
Plaçons nous dans le repère orthonormé $(D,{DC}↖{→},{DH}↖{→},{DA}↖{→})$.
Nous savons que D( 0 ; 0 ; 0 ) A( 0 ; 0 ; 1 )
${AG}↖{→}$( 1 ; 1 ; -1 ).
Soit Q le point situé à l'intersection de la droite (AG) et du plan (EBD).
Il existe un réel $k$ tel que ${AQ}↖{→}=k {AG}↖{→}$. Pourquoi?
Déterminer la valeur de $k$ et les coordonnées de Q.
Calculer la distance entre A et le plan (EBD).
Quel est le point du plan (EBD) situé à une distance de 0,5 du point A?
Corrigé
La droite (AG) passe par A et elle a pour vecteur directeur ${AG}↖{→}$.
Or Q est sur (AG).
Donc il existe un réel $k$ tel que ${AQ}↖{→}=k {AG}↖{→}$.
Posons Q( $x$ ; $y$ ; $z$ )
On a alors: ${AQ}↖{→}$( $x$ ; $y$ ; $z-1$ )
Par ailleurs, on a vu que: ${AG}↖{→}$( 1 ; 1 ; -1 )
Et comme ${AQ}↖{→}=k {AG}↖{→}$, on obtient: $\{\table x=k;y=k;z-1=-k$ Soit: $\{\table x=k;y=k;z=1-k$
On obtient alors: Q( $k$ ; $k$ ; $1-k$ ) et ${DQ}↖{→}$ ( $k$ ; $k$ ; $1-k$ )
Par ailleurs, comme la droite (AG), de vecteur directeur ${AG}↖{→}$, est orthogonale au plan (EBD), et comme Q et D appartiennent au plan (EBD),
les vecteurs ${AG}↖{→}$ et ${DQ}↖{→}$ sont orthogonaux.
Donc ${AG}↖{→}.{DQ}↖{→}=0$
Soit: $1×k+1×k+(-1)×(1-k)=0$
Et par là: $3k-1=0$ Et donc: $k={1}/{3}$
Donc finalement, on obtient: Q( ${1}/{3}$ ; ${1}/{3}$ ; ${2}/{3}$ )
Comme la droite (AG), de vecteur directeur ${AG}↖{→}$, est orthogonale au plan (EBD), et comme (AG) et (EBD) se coupent en Q,
le point Q est le projeté orthogonal de A sur le plan (EBD),
et par là, la distance entre A et le plan (EBD) est la distance AQ.
On obtient facilement ${AQ}↖{→}$( ${1}/{3}$ ; ${1}/{3}$ ; $-{1}/{3}$ )
Et par là: $AQ=√{({1}/{3})^2+({1}/{3})^2+(-{1}/{3})^2}=√{{1}/{3}}≈0,58$
Q, projeté orthogonal de A sur le plan (EBD) est le point de (EBD) le plus proche de A.
Et comme $AQ≈0,58$, aucun point de (EBD) ne peut être situé à une distance de 0,5 du point A.
Savoir faire
Quel est l'intérêt du produit scalaire dans l'espace?
Il permet de déterminer l'angle entre 2 vecteurs, en particulier l'angle droit.
Il permet de caractériser facilement les points d'un plan dont on connait un point et un vecteur normal.
Mais attention, la formule de calcul analytique du produit scalaire nécessite un repère orthonormal!