 Fonctions sinus et cosinus
Fonctions sinus et cosinus
Un conseil: revoir le cours sur les fonctions sin et cos de la classe de première!
Quelques rappels de Première.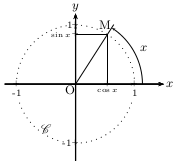
Pour tout réel $x$:
$-1≤\cos x≤1$ $-1≤\sin x≤1$ $\cos^2 x+\sin^2 x=1$
$\cos(-x)=\cos x$ $\sin (-x)=-\sin x$
$\cos(π-x)=-\cos x$ $\sin(π-x)=\sin x$
$\cos(π+x)=-\cos x$ $\sin(π+x)=-\sin x$
$\cos({π}/{2}-x)=\sin x$ $\sin({π}/{2}-x)=\cos x$
Pour tout $k$ entier relatif $\sin (x+2kπ)=\sin x$ $\cos (x+2kπ)=\cos x$
Exemple
Résoudre l'équation $\cos x=0,5$ sur $[-π;π]$
Résoudre l'inéquation $\cos x$>$0,5$ sur $[-π;π]$
Résoudre l'inéquation $\cos x$<$0,5$ sur $[-π;π]$
Corrigé
Dans chacun des 3 cas suivants, on résout sur l'intervalle $[-π;π]$
On repère les réels concernés à l'aide du cercle trigonométrique.
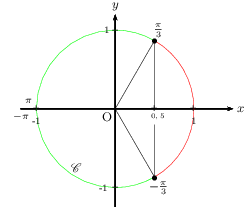
$\cos x=0,5$ $ ⇔$ $\cos x=\cos {π}/{3}$ $⇔$ $x={π}/{3}$ ou $x=-{π}/{3}$
Donc $\S=\{-{π}/{3};{π}/{3}\}$ sur l'intervalle $[-π;π]$
$\cos x$>$0,5$ $ ⇔$ $\cos x$>$\cos {π}/{3}$ $⇔$ $-{π}/{3}$<$x$<${π}/{3}$
Donc $\S=]-{π}/{3};{π}/{3}[$ sur l'intervalle $[-π;π]$
$\cos x$<$0,5$ $ ⇔$ $\cos x$<$\cos {π}/{3}$ $⇔$ $-π≤x$<$-{π}/{3}$ ou ${π}/{3}$<$x≤π$
Donc $\S=[-π;-{π}/{3}[∪]{π}/{3};π]$ sur l'intervalle $[-π;π]$
Définition
La fonction sinus est la fonction définie sur $\R$ qui,
à tout réel $x$ associe $\sin x$.
La fonction cosinus est la fonction définie sur $\R$ qui,
à tout réel $x$ associe $\cos x$.
Propriétés
La fonction $\sin x$ admet pour dérivée $\cos x$ sur $\R$. Ainsi: $(\sin x)\,'=\cos x$.
La fonction $\cos x$ admet pour dérivée $-\sin x$ sur $\R$. Ainsi: $(\cos x)\,'=-\sin x$.
 Exemple
Exemple
Soit $f$ définie sur $]-{π}/{2};{π}/{2}[$ par $f(x)={\sin x}/{\cos x}$.
Dériver $f$.
Corrigé
On pose $f={u}/{v}$ avec $u=\sin x$ et $v=\cos x$.
Donc $f\,'={u'v-uv'}/{v^2}$ avec $u'=\cos x$ et $v'=-\sin x$.
Et par là $f\,'(x)={\cos x × \cos x-\sin x ×(-\sin x)}/{(\cos x)^2}={\cos^2 x+\sin^2 x}/{\cos^2 x}={1}/{\cos^2x}$.
Propriétés
Les fonctions sinus et cosinus sont continues sur $\R$.
Les fonctions sinus et cosinus sont périodiques de période $2π$ sur $\R$.
Par conséquent, pour tout $x$ réel et tout $k$ entier relatif, on a:
$\sin (x+2kπ)=\sin x$
et $\cos (x+2kπ)=\cos x$.
Et par là, dans un repère $(O,i↖{→},j↖{→})$, les courbes représentatives des fonctions sinus et cosinus sont invariantes par toute translation de vecteur $k2πi↖{→}$.
La fonction sinus est impaire sur $\R$.
Par conséquent, pour tout $x$ réel, $\sin(-x)=-\sin x$.
Et par là, la courbe représentative de la fonction sinus est symétrique par rapport à l'origine.
La fonction cosinus est paire sur $\R$.
Par conséquent, pour tout $x$ réel, $\cos(-x)=\cos x$.
Et par là, dans un repère orthogonal, la courbe représentative de la fonction cosinus est symétrique par rapport à l'axe des ordonnées.
Les fonctions sinus et cosinus vérifient les tableaux de variation ci-dessous.
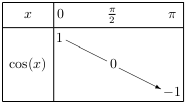
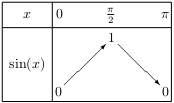
Les fonctions sinus et cosinus vérifient les tableaux de signes ci-dessous.
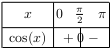

Les fonctions sinus et cosinus vérifient les tableaux de valeurs ci-dessous.
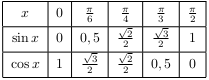
Ces tableaux de valeurs s'étendent à $[0;π]$ en utilisant les angles associés, qui fournissent les égalités: $\sin (π-x)=\sin (x)$ et $\cos (π-x)=-\cos (x)$.
On obtient chacune des courbes ci-dessous à partir d'un tracé sur $[0;π]$, étendu par symétrie sur $[-π;π]$, et répété à l'infini par translations successives.
Ces courbes s'appellent des sinusoïdes.
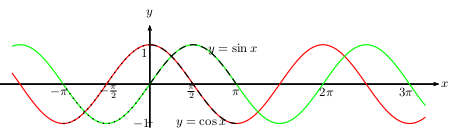
Exemple
Soit $\C_f$ la courbe représentative de la fonction $f$ définie sur $[0;π]$ par $f(x)=\cos^2 x+\cos(2x)$.
Conjecturer le sens de variation de $f$, puis démontrer cette conjecture.
On peut, si besoin, utiliser l'égalité: $\sin(2x)=2\sin x\cos x$.
Corrigé
L'allure de $\C_f$, tracé ci-dessous, laisse à penser que $f$ est décroissante sur $[0;{π}/{2}]$, et croissante sur $[{π}/{2};π]$.
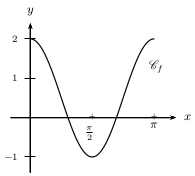
On rappelle que la dérivée de $u^2$ est $2u'u$ et que la dérivée de $g(ax+b)$ est $ag'(ax+b)$.
On pose $f=u^2+g(2x+0)$ avec $u=\cos x$ et $g(y)=\cos y$.
Donc $f\,'=2u'u+2g'(2x+0)$ avec $u'=-\sin x$ et $g'(y)=-\sin y$.
Et par là: $f\,'(x)=2×(-\sin x)×\cos x+2×(-\sin(2x))=-2\sin x\cos x-2\sin(2x)$.
On rappelle que: $\sin(2x)=2\sin x\cos x$.
Donc: $f\,'(x)=-2\sin x\cos x-2×2\sin x\cos x=-6\sin x \cos x$.
Sur $[0;{π}/{2}]$, $\cos x≥0$ et $\sin x ≥0$, et par là $f\,'(x)≤0$.
Donc $f$ est décroissante sur $[0;{π}/{2}]$.
Sur $[{π}/{2};π]$, $\cos x≤0$ et $\sin x ≥0$, et par là $f\,'(x)≥0$.
Donc $f$ est croissante sur $[{π}/{2};π]$.
Limite de référence
$\lim↙{x→0}{\sin x}/{x}=1$