Succession d'épreuves indépendantes, schéma de Bernoulli
A SAVOIR: le cours sur Succession d'épreuves indépendantes, schéma de Bernoulli
Exercice 2
Partie A
Les 9 lettres du mot EXERCICES sont mises dans une urne.
On tire au hasard 3 lettres de l'urne, successivement mais avec remise.
On compte le nombre de voyelles obtenues.
- Cette situation est-elle modélisée par un schéma de Bernoulli?
- Représenter la situation par un arbre pondéré.
- Soit A:" aucune voyelle n'est piochée"
Soit B:" exactement une voyelle a été piochée"
Soit C:" on a pioché plus de voyelles que de consonnes"
Déterminer les probabilités de ces 3 événements.
Partie B
Répondre aux mêmes questions que celles de la partie A dans le cas où les tirages sont sans remise.
Solution...
Corrigé
Partie A
- On répète 3 fois de manière indépendante une expérience à 2 issues:
V: "la lettre est une voyelle"
C:" la lettre est une consonne".
On a $p(V)={4}/{9}$.
Nous sommes donc en présence d'un schéma de Bernoulli de paramètres $n=3$ et $p={4}/{9}$ - Voici un arbre pondéré convenable.
-
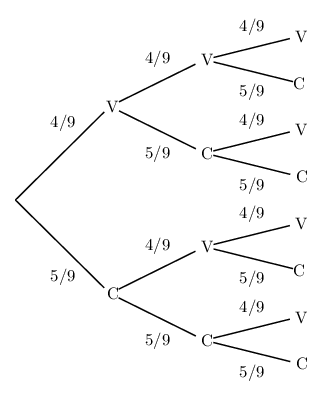
$p(A)=p((C,C,C))=(1-p)^3={125}/{729}≈0,17$
$p(B)=p((V,C,C))+p((C,V,C))+p((C,C,V))=3p(1-p)^2={100}/{243}≈0,41$
$C=\ov{A∪B}$ et A et B sont incompatibles.
Donc $p(C)=1-(p(A)+p(B))={304}/{729}≈0,42$
Partie B
- On répète 3 fois une expérience à 2 issues:
V: "la lettre est une voyelle"
C:" la lettre est une consonne".
Mais les tirages ne sont plus indépendants.
Nous ne sommes donc pas en présence d'un schéma de Bernoulli. - Voici un arbre pondéré convenable.
-
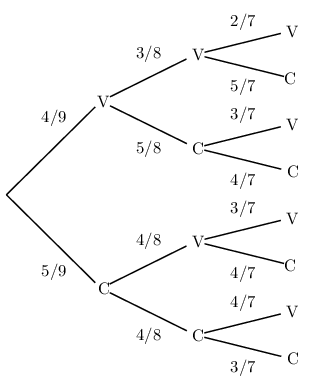
$p(A)=p((C,C,C))={5}/{9} ×{4}/{8} ×{3}/{7}={5}/{42}≈0,12$
$p(B)=p((V,C,C))+p((C,V,C))+p((C,C,V))={4}/{9} ×{5}/{8} ×{4}/{7}+{5}/{9} ×{4}/{8} ×{4}/{7}+{5}/{9} ×{4}/{8} ×{4}/{7}={10}/{21}≈0,48$
$C=\ov{A∪B}$ et A et B sont incompatibles.
Donc $p(C)=1-(p(A)+p(B))={17}/{42}≈0,40$