 Succession d'épreuves indépendantes, schéma de Bernoulli
Succession d'épreuves indépendantes, schéma de Bernoulli
Un conseil: revoir le cours sur les probabilités conditionnelles de la classe de première!
I Succession d'épreuves indépendantes
Définition
$n$ épreuves successives sont indépendantes lorsque le résultat de l'une n'influe pas sur le résultat de l'autre.
Propriété
On considère une succession de $n$ épreuves indépendantes.
Pour toute liste $(A_1, A_2,...,A_n)$ d'événements concernant les $n$ épreuves successives, on a:
$p(A_1∩A_2∩...∩A_n)=p(A_1)×p(A_2)×...×p(A_n)$
Une telle succession peut se représenter par un arbre de probabilité.
Exemple
On jette un dé, puis on tire un jeton d'un sac contenant les jetons R, V , B et J, puis on jette une pièce.
Soit G: "le résultat du dé vaut au moins 5"
Soit R: "le jeton est R"
Soit F: "la pièce est tombée sur Face"
Soit P: "la pièce est tombée sur Pile"
Modéliser l'expérience.
Nous sommes en présence de 3 épreuves indépendantes.
On a: $p(G)={2}/{6}={1}/{3}$ et $p(R)={1}/{4}$ et $p(F)={1}/{2}$
Représentation par un arbre de probabilité.
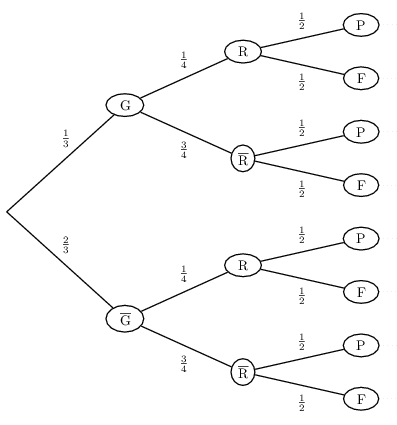
On a alors, par exemple: $p(G∩R∩F)=p(G)×p(R)×p(F)={1}/{3}×{1}/{4}×{1}/{2}={1}/{24}$
II Schéma de Bernoulli et loi binomiale
Définition
Une épreuve de Bernoulli de paramètre $p$ est une expérience ayant 2 issues, appelées "succès" et "échec" telle que la probabilité de "succès" vaut $p$.
La loi de Bernoulli est la loi de la variable aléatoire X qui code le résultat d'une épreuve de Bernoulli de paramètre $p$ de la façon suivante:
$p(X=1)=p(« succès »)=p$ $p(X=0)=p(« échec »)=1-p$
Exemple
On lance une pièce. Soit X la variable aléatoire qui vaut 1 si on a obtenu Pile, et 0 si on a obtenu Face.
Si on appelle succès l'obtention de Pile, et échec l'obtention de Face, alors nous sommes en présence d'une épreuve de Bernoulli, et X suit la loi de Bernoulli.
On a ici: $p(X=1)=p(\text"obtenir Pile")=0,5$ $p(X=0)=p(\text"obtenir Face")=1-0,5=0,5$
Définition
Un schéma de Bernoulli de paramètres n et p est l'expérience consistant à répéter $n$ fois de manière indépendante une épreuve de Bernoulli de paramètre $p$.
Un schéma de Bernoulli se représente à l'aide d'un arbre pondéré
où les noeuds ont chacun 2 branches
et où les mêmes probabilités $p$ et $1-p$ sont répétées sur les couples de branches.
Définition
On considère un schéma de Bernoulli de paramètres $n$ et $p$.
La loi de probabilité de la variable aléatoire X égale au nombre de succès au cours de ces $n$ épreuves
est appelée loi binomiale de paramètres $n$ et $p$.
On la note: $B (n,p)$.
Exemple
Une usine fabrique des composants électriques.
On prélève au hasard 3 composants dans la production de la journée.
On suppose que les prélèvements sont indépendants l'un de l'autre,
et que la probabilité qu'un composant soit conforme au cahier des charges est égale à 0,84.
- Représenter l'expérience par un arbre pondéré.
- Enumérer tous les cas possibles dans un produit cartésien..
-
Soit X la variable aléatoire donnant le nombre de composants conformes parmi les 3.
Que dire de X? - Quelle est la probabilité que le premier composant soit conforme, mais pas les 2 suivants?
- Quelle est la probabilité que le second composant soit conforme, mais pas les 2 autres?
Corrigé
- arbre pondéré:
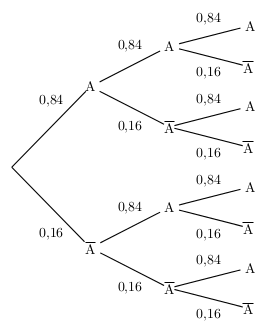
- Si on appelle $E=\{A,A↖{-}\}$, alors les 8 issues possibles sont les éléments du produit cartésien $ExExE$.
On a: $ExExE=\{(A,A,A),(A,A,A↖{-}),(A,A↖{-},A),(A,A↖{-},A↖{-}),(A↖{-},A,A),(A↖{-},A,A↖{-}),(A↖{-},A↖{-},A),(A↖{-},A↖{-},A↖{-})\}$ - Chacun des prélèvements constitue une épreuve de Bernoulli de paramètre $p=0,84$ et dont le succès est A.
Les 3 prélèvements sont indépendants, et X compte le nombre de succès.
Par conséquent X est une binomiale de paramètres 3 et 0,84.
Soit: $X=B (\,3\,;\,0,84\,)$ - On cherche: $p((A,A↖{-},A↖{-}))=p(A)×p(A↖{-})×p(A↖{-})=0,84×0,16×0,16=0,021504$
- On cherche: $p((A↖{-},A,A↖{-})==p(A↖{-})×p(A)×p(A↖{-})=0,16×0,84×0,16=0,021504$
On retrouve le résultat précédent.
Propriété
Soit $n∈\ℕ^{*}$ et $k∈\ℕ$ avec $0≤ k≤ n$.
Le nombre de chemins réalisant $k$ succès pour $n$ répétitions
sur l'arbre d'un schéma de Bernoulli de paramètres n et p se note $(\table n; k)$
C'est le nombre de combinaisons de $k$ objets parmi $n$; on l'appelle aussi coefficient binomial $(\table n; k)$ (et on dit "k parmi n").
Par convention: $(\table 0; 0)=1$
Les coefficients binomiaux sont étudiés de façon plus approfondie dans le chapitre Combinatoire et dénombrement.
Si besoin, clique ICI pour revoir le cours sur les combinaisons.
On obtient directement les coefficients binomiaux avec les calculatrices:
Casio: OPTN PROB n nCr k
TI: MATH PRB n Combinaison k
Exemple
On reprend l'exemple précédent.
Dénombrer le nombre d'événements donnant exactement 1 composant conforme.
Citer les tous.
Que dire de leurs probabilités?
En déduire la probabilité d'avoir exactement 1 composant conforme.
Corrigé
On cherche le nombre de chemins réalisant $1$ succès pour $3$ répétitions
sur l'arbre précédent.
Il est égal à $(\table 3; 1)=3$
Il s'agit de $(A,A↖{-},A↖{-})$, $(A↖{-},A,A↖{-})$ et $(A↖{-},A↖{-},A)$.
On a: $p((A,A↖{-},A↖{-}))=p((A↖{-},A,A↖{-}))=p((A↖{-},A↖{-},A))=p(A)×p(A↖{-})×p(A↖{-})=0,021504$ (vu précédemment)
Les probabilités des ces 3 événements sont égales.
La probabilité d'avoir exactement 1 composant conforme vaut donc $3×0,021504=0,064512$
Expression de la loi binomiale
Si $X=B (n,p)$, et $0≤ k≤ n$, alors $p(X=k)=(\table n; k)\,p^k(1-p)^{n-k}$ .
En pratique, on obtient directement les valeurs de $p(X=k)$ avec les calculatrices:
Casio: STAT DIST BinomialPD($k,n,p$)
TI: 2nd distrib binomFdp($n,p,k$)
De même pour les valeurs de $p(X≤k)$:
Casio: STAT DIST BinomialCD($k,n,p$)
TI: 2nd distrib binomFrép($n,p,k$)
Exemple
On reprend encore l'exemple précédent.
- Donner la formule donnant la probabilité qu'exactement 2 composants soient acceptés, puis déterminer la valeur de cette probabilité (arrondie à 0,0001 près).
- Déterminer la probabilité (arrondie à 0,0001 près) qu'au moins 1 composant soit accepté.
Corrigé
-
On cherche $p(X=2)$. On a: $p(X=2)=(\table 3; 2)\,0,84^2(1-0,84)^{3-2}=3×0,84^2×0,16≈0,3387$.
A la calculatrice, on peut obtenir directement: $p(X=2)≈0,3387$. -
On cherche $p(X≥1)$.
Or $p(X≥1)=1-p(X\text"<"1)=1-p(X≤0)=1-p(X=0)$.
Et à la calculatrice, on obtient: $p(X=0)≈0,0041$.
Donc $p(X≥1)≈0,9959$.
Propriété
Si $X$ suit une loi binomiale de paramètre $n$ et $p$, alors:
son espérance est: $E(X)=np$
sa variance est: $V(X)=np(1-p)$
son écart-type est: $σ(X)=√ {np(1-p)}$