Combinatoire et dénombrement
A SAVOIR: le cours sur Combinatoire et dénombrement
Exercice 10
Tout entier naturel $n$ peut s'écrire sous la forme d'une somme unique de puissances de 2 comme suit:
$n=a_k×2^k+a_{k-1}×2^{k-1}+a_{k-2}×2^{k-2}+...+a_2×2^2+a_1×2^1+a_0×2^0$,
où $k$ dépend de $n$,
et où $a_k=1$,
et où tous les $a_i$ pour $i$ entre 0 et $k-1$ valent soit 0, soit 1.
Par exemple: $0=0×2^0$ $1=1×2^0$ $2=1×2^1+0×2^0$
$6=1×2^2+1×2^1+0×2^0$ $8=1×2^3+0×2^2+0×2^1+0×2^0$ $17=1×2^4+0×2^3+0×2^2+0×2^1+1×2^0$
La suite des $a_i$ pour $i$ allant de $k$ à 0 donne l'écriture binaire du nombre $n$ considéré.
En cas d'ambiguïté, l'indice (dec) ou (bin) permet de savoir si l'écriture considérée est décimale ou binaire.
Par exemple: $0_(dec)=0_(bin)$ $1_(dec)=1_(bin)$ $2_(dec)=10_(bin)$
$6_(dec)=110_(bin)$ $8_(dec)=1000_(bin)$ $17_(dec)=10001_(bin)$
- Donner l'écriture binaire de 13
- Donner l'écriture décimale de $10101_(bin)$
- En PYTHON, l'instruction L.reverse() retourne la liste L en ayant inversé l'ordre de ses éléments.
Par exemple, si L=[1,2,3], alors L.reverse() retourne [3,2,1]
En PYTHON, l'instruction a//b retourne le quotient de la division euclidienne de a par b.
En PYTHON, l'instruction a%b retourne le reste de la division euclidienne de a par b.
Une suite de division euclidiennes par 2 fournit l'écriture binaire de n'importe quel naturel. Il suffit de noter les restes successifs, qui donneront dans l'ordre $a_0$, $a_1$ ,...etc...
Par exemple: $6=2×3+0$ donne $a_0=0$, puis: $3=2×1+1$ donne $a_1=1$, puis: $1=2×0+1$ donne $a_2=1$.
On vient de montrer que: $6=1×2^2+1×2^1+0×2^0$.
Et par là: $6_(dec)=110_(bin)$
Ecrire en PYTHON une fonction binaire(x) qui retourne une liste du type $[a_k, a_{k-1},...,a_1, a_0]$ donnant l'écriture en binaire de l'entier naturel $x$.
Par exemple, binaire(6) retourne [1,1,0] - Une écriture binaire peut être précédée d'autant de 0 que l'on veut.
Par exemple, 110 et 00110 codent toutes les deux le nombre 6.
Ecrire en PYTHON une fonction binaireF(x,n) qui retourne une liste de longueur n donnant l'écriture en binaire de l'entier naturel $x$; la liste commencera donc éventuellement par des 0.
Par exemple, binaireF(6,5) retourne [0,0,1,1,0] - L'écriture binaire d'un entier naturel étendue à n chiffres correspond à un n-uplet.
Par exemple, $6_(dec)=110_(bin)$ correspond au 3-uplet (1,1,0).
Et $6_(dec)=00110_(bin)$ correspond au 5-uplet (0,0,1,1,0).
Ecrire en PYTHON une fonction liste_n_uplet(n) qui retourne une liste de tous les n-uplets de $\{0,1\}$.
Par exemple, liste_n_uplet(2) retourne [[0, 0], [0, 1], [1, 0], [1, 1]] - On a vu dans un exemple du cours comment associer à chaque n-uplet de $\{0,1\}$ une partie d'un ensemble à n éléments.
Ecrire en PYTHON une fonction parties(L) qui retourne une liste du type $[L_1,L_2,...,L_p]$,
où $L$ est une liste donnant les éléments d'un ensemble E,
où $p$ est le nombre de parties de E,
où $L_1$, $L_2$,..., $L_p$ sont des listes donnant les éléments des différentes parties de E.
Par exemple, si $E=\{1,2\}$, alors L=[ 1 , 2 ],
et parties(L) retourne la liste [ [] , [2] , [1] , [1 , 2] ]
Vérifier que votre programme est correct en affichant les parties de $E=\{1,2,3\}$
Solution...
Corrigé
- On a: $13=8+4+1=1×2^3+1×2^2+0×2^1+1×2^0$. Donc: $13_(dec)=1101_(bin)$
- On considère $10101_(bin)$. On calcule alors: $1×2^4+0×2^3+1×2^2+0×2^1+1×2^0=16+4+1=21$
Donc: $10101_(bin)=21_[dec)$ -
Voici une fonction binaire(n) qui retourne une liste donnant l'écriture en binaire de l'entier naturel $n$.
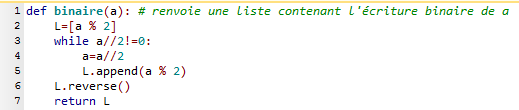
- Voici une fonction binaireF(x,n) qui retourne une liste de longueur n donnant l'écriture en binaire de l'entier naturel $x$.
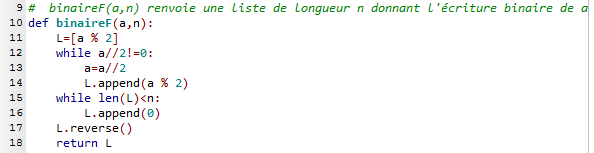
On aurait pu utiliser l'instruction L=binaire(a) à l'intérieur de cette définition pour remplacer les lignes 11 à 14, mais il aurait fallu ensuite utiliser l'instruction L.reverse() pour de nouveau inverser l'ordre des éléments de L, ce qui n'estpas très habile... - Voici une fonction liste_n_uplet(n) qui retourne une liste de tous les n-uplets de $\{0,1\}$.
La variable nombre contient le nombre de n-uplets à générer.
Chacun d'eux est associé à l'écriture binaire à n chiffres d'un naturel compris entre 0 et nombre-1
Par exemple, liste_n_uplet(2) retourne une liste de tous les 2-uplets de $\{0,1\}$.
Ces 2-uplets sont $2^2=4$.
Le premier (0,0) est associé à $0_(dec)=00_(bin)$.
Le second (0,1) associé à $1_(dec)=01_(bin)$.
Le troisième (1,0) associé à $2_(dec)=10_(bin)$.
Le quatrième (1,1) associé à $3_(dec)=11_(bin)$. -
Voici une fonction parties(L) qui retourne une liste donnant les parties de l'ensemble associé à L. ,
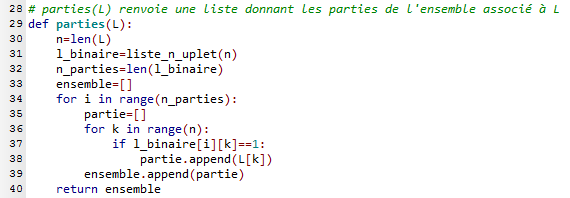
Pour afficher les parties de $E=\{1,2,3\}$, il suffit d'ajouter ces deux lignes à la suite du fichier donnant les fonctions précédentes, et d'exécuter le programme.
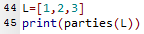
Il s'affiche dans la console:
[[], [3], [2], [2, 3], [1], [1, 3], [1, 2], [1, 2, 3]]
On peut aussi taper les mêmes instructions directement dans la console.
Pour les experts!
Le programme qui suit propose un affichage plus convivial des parties de l'ensemble E, à condition que E soit constitué d'entiers naturels.
Si L est une liste dont les éléments sont des chaînes de caractères, alors l'instruction ' truc '.join(L) retourne une chaîne composée des éléments de L séparés par la chaîne ' truc '.
Par exemple, si L=('un','bizarre'), alors 'truc'.join(L) renvoie 'un truc bizarre'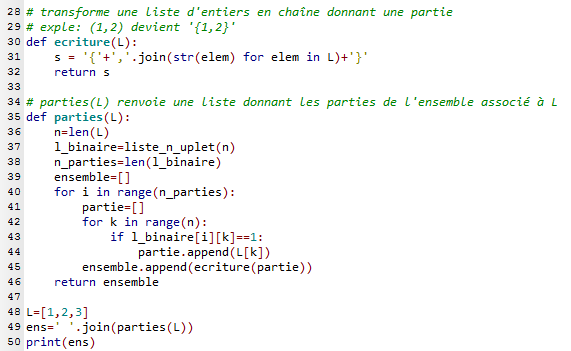
Notre programme affiche {} {3} {2} {2,3} {1} {1,3} {1,2} {1,2,3} dans la console.