Corrigé

1. 1. Soit $n$ un naturel.
      On a: $u_{n+1}-u_n={1}/{0!}+{1}/{1!}+{1}/{2!}+...+{1}/{n!}+{1}/{(n+1)!}-{1}/{0!}-{1}/{1!}-{1}/{2!}-...-{1}/{n!}$
      Soit: $u_{n+1}-u_n={1}/{(n+1)!}$
      Or résultat est strictement positif. Et c'est vrai pour tout naturel $n$.
      Donc $(u_n)$ est strictement croissante.
   
   
   2. Soit $P_n$: ${1}/{n!}≤{1}/{2^{n-1}}$
      Démontrons par récurrence que, pour tout naturel $n$ non nul, la propriété $P_n$ est vraie.
      Initialisation: On a: ${1}/{1!}=1$ et ${1}/{2^{1-1}}={1}/{2^{0}}=1$.
      On a bien ${1}/{1!}≤{1}/{2^{1-1}}$. Donc $P_{1}$ est vraie.
      Hérédité:
      Soit $n$ un entier naturel non nul, supposons que $P_n$ soit vraie.
      On a donc: ${1}/{n!}≤{1}/{2^{n-1}}$.
      Donc: ${1}/{n+1} ×{1}/{n!}≤{1}/{n+1} ×{1}/{2^{n-1}}$. ( on a multiplié chaque membre par un nombre strictement positif ${1}/{n+1}$ )
      On obtient donc: ${1}/{(n+1)!}≤{1}/{(n+1)×2^{n-1}}$
      
      Or, comme $1≤n$, on a: $2≤n+1$, et donc: $2×2^{n-1}≤(n+1)×2^{n-1}$
      Et par là: ${1}/{(n+1)×2^{n-1}}≤{1}/{2×2^{n-1}}$  ( deux nombres strictement positifs et leurs inverses sont dans l'ordre inverse )
      Soit: ${1}/{(n+1)×2^{n-1}}≤{1}/{2^{n}}$.
      
      Par conséquent, on en déduit finalement que: ${1}/{(n+1)!}≤{1}/{2^{n}}$.
      Donc $P_{n+1}$ est vraie.
      Conclusion: pour tout naturel $n$ non nul, ${1}/{n!}≤{1}/{2^{n-1}}$.
      
      
   
   
   3. D'après le résultat précédent, pour tout naturel $k$ non nul, on a: ${1}/{k!}≤{1}/{2^{k-1}}$.
      Donc, pour tout naturel $n$ non nul: ${1}/{1!}+{1}/{2!}+...+{1}/{n!}≤{1}/{2^{1-1}}+{1}/{2^{2-1}}+...+{1}/{2^{n-1}}$
      Or: $1+q+q^2+...+q^{n-1}={1-q^n}/{1-q}$ pour $q≠1$
      Ici: $q={1}/{2}$, et par là, on a, on obtient: ${1}/{1!}+{1}/{2!}+...+{1}/{n!}≤{1-({1}/{2})^n}/{1-{1}/{2}}$
      Soit: ${1}/{1!}+{1}/{2!}+...+{1}/{n!}≤{1-0,5^n}/{{1}/{2}}$
      Soit: ${1}/{1!}+{1}/{2!}+...+{1}/{n!}≤2(1-0,5^n)$
      Et par là, en sommant 1 à chaque membre: $u_n≤1+2(1-0,5^n)$
      Soit: $u_n≤3-2×0,5^n$
      Ceci est également vrai pour $n=0$ (car $u_0=1$ et $3-2×0,5^0=1$)
      Finalement: pour tout naturel $n$, on a: $u_n≤3-2×0,5^n$
   
   
   4. Comme $u_n≤3-2×0,5^n$, on en déduit immédiatement que: $u_n≤3$
      La suite $(u_n)$ est donc majorée.
      Or la suite $(u_n)$ est strictement croissante.
      Donc la suite $(u_n)$ est convergente.


2. 1. Voici une fonction factorielle(n) qui retourne la valeur de $n!$ pour tout naturel $n$.
      
   
   
   2. Voici une fonction u(n) qui retourne la valeur de $u_n$ pour tout naturel $n$.
      
      On aurait commencer le programme par from math import factorial
      et remplacer factorielle(k) par factorial(k) dans le programme, mais cela n'aurait pas respecté l'énoncé!
   
   
   3. Le programme nous donne:    u(5)$≈$2.7166666666666663    u(10)$≈$2.7182818011463845
      u(100)$≈$2.7182818284590455    et    u(1000)$≈$2.7182818284590455
      
      On conjecture que $\lim↙{n→+∞}u_n=e$.
   
   
   4. Voici une fonction min(delta) qui retourne le plus petit entier $n$ à partir duquel $|u_n-l| ≤ delta$, où $delta$ est un réel strictement positif.
      
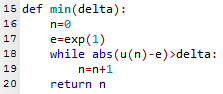
      Evidemment, pour que PYTHON comprenne ce que représente exp(1), il suffit de commencer le programme par from math import exp
      
   
   
   5. Jean affirme qu'un tel entier $n$ existe car $(u_n)$ est strictement croissante.
      Jean a tort. Un tel entier $n$ existe car $\lim↙{n→+∞}u_n=e$.
      Le fait que $(u_n)$ soit strictement croissante nous assure que le programme proposé renvoie bien le plus petit entier convenable.