Combinatoire et dénombrement
A SAVOIR: le cours sur Combinatoire et dénombrement
Exercice 2
Soit E un ensemble à $n$ éléments (avec $n$ entier non nul).
Combien y a-t-il de couples (A,B) de parties de E tels que $A∪B=E$ et $A∩B=∅$ ?
- On suppose que A est une partie à $p$ éléments de E.
Combien y a-t-il de parties B de E tels que $A∪B=E$ ?
Solution...
Corrigé
- Un couple (A,B) est convenable si et seulement si B est le complémentaire de A dans E.
Donc un couple est convenable si et seulement si il est du type $(A,\ov {A})$.
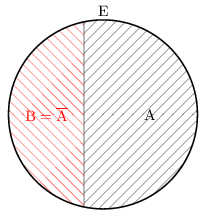
Il y a donc autant de couples $(A,\ov {A})$ que de parties A de E.
Et, comme E est un ensemble à $n$ éléments, il y en a $2^n$. - Une partie B est convenable si et seulement si $B=\ov {A}∪C$, où C est une partie de A.
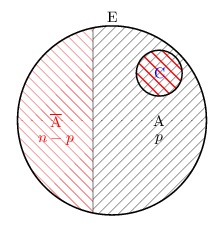
Il y a donc autant de parties B convenables que de parties C de A.
Et, comme A est un ensemble à $p$ éléments, il y en a $2^p$.