 Continuité
Continuité
A SAVOIR: le cours sur la continuité
Exercice 2
Soit $f$ la fonction définie sur $\[1;2\]$ par $f(x)=x^3+x$.
Montrer que l'équation $f(x)=5$ admet une solution unique α sur $\[1;2\]$, puis déterminer un encadrement de α d'amplitude 0,1.
Corrigé
$f\,'(x)=3x^2+1$.
Etudions le signe de cette dérivée.
$x^2 ≥ 0$ (c'est un carré).
Donc $3x^2 ≥ 0$, et par là: $3x^2+1$>0.
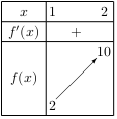
D'où le tableau de variation de $f$ ci-contre.
D'après ce tableau de variation, la fonction $f$ est continue et strictement croissante sur $\[1;2\]$.
Or 5 est un nombre compris entre $f(1)=2$ et $f(2)=10$,
Donc, d'après le théorème de la bijection, l'équation $f(x)=5$ admet une unique solution α sur $\[1;2\]$.
Déterminons un encadrement de α par essais successifs à l'aide de la calculatrice.
Nous remplissons ainsi le tableau de valeurs suivant:

Les valeurs sont arrondies à $10^{-3}$ près.
L'encadrement cherché est: $1,5$<α<$1,6$.
Et comme $1,6-1,5=0,1$, l'amplitude est bien égale à 0,1.