 Continuité
Continuité
A SAVOIR: le cours sur la continuité
Exercice 3
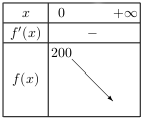
Soit $f$ la fonction définie sur $\[0;+∞[$ et vérifiant le tableau de variations ci-contre.
On sait de plus que $f(100)=3$.
Montrer que l'équation $f(x)=50$ admet une solution unique sur $\[0;+∞[$.
Corrigé
D'après ce tableau de variation, la fonction $f$ est continue et strictement décroissante sur $\[0;+∞[$, et donc en particulier sur $\[0;100\]$.
Or 50 est un nombre compris entre $f(0)=200$ et $f(100)=3$,
Donc, d'après le théorème de la bijection, l'équation $f(x)=50$ admet une unique solution sur $\[0;100\]$.
De plus, comme $f$ est strictement décroissante sur $\[0;∞[$, si $x$>100, alors $f(x)$<$f(100)$; c'est à dire que si $x$>100, alors $f(x)$<3.
Par conséquent, l'équation $f(x)=50$ ne peut avoir de solution sur $\]100;∞[$.
Finalement, l'équation $f(x)=50$ admet une solution unique sur $\[0;∞[$.