Continuité
A SAVOIR: le cours sur la continuité
Exercice 4
Soit $f$ la fonction définie sur $\[0;10\]$ telle que $f(0)=30$ et $f(10)=2$.
Est-il certain que les propositions suivantes soient vraies? (inutile de justifier)
Lorsqu'une proposition est fausse, tracer la courbe représentative d'une fonction $f$ présentant un contre-exemple.
1. L'équation $f(x)=15$ admet au moins une solution sur $\[0;10\]$.
2. L'équation $f(x)=15$ admet une unique solution sur $\[0;10\]$.
3. L'équation $f(x)=50$ n'admet pas de solution sur $\[0;10\]$.
Corrigé
Toutes les propositions peuvent être fausses.
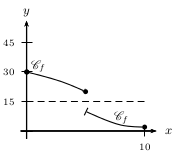figure 1
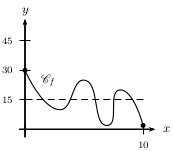figure 2
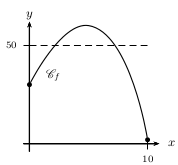figure 3
Figure 1: L'équation $f(x)=15$ n'admet pas de solution sur $\[0;10\]$.
Remarquons que ni le théorème des valeurs intermédiaires, ni le théorème de la bijection ne peuvent s'appliquer car $f$ n'est pas continue sur $\[0;10\]$.
Figure 2: L'équation $f(x)=15$ admet cinq solutions sur $\[0;10\]$.
Remarquons que le théorème de la bijection ne peut s'appliquer car $f$ n'est pas strictement monotone sur $\[0;10\]$.
Figure 3: L'équation $f(x)=50$ admet deux solutions sur $\[0;10\]$.
Remarquons que ceci n'est démontrable ni avec le théorème des valeurs intermédiaires,
ni avec le théorème de la bijection;
ces théorèmes ne peuvent s'appliquer car le nombre 50 n'est pas entre $f(0)$ et $f(10)$.