Corrigé

1.a. Comme $2\text">"0$ et $\lim↙{x→+∞}x-1=+∞$ et $\lim↙{x→+∞}e^x=+∞$,
on en déduit que $\lim↙{x→+∞}2(x-1)e^x=+∞$ (limite d'un produit).
Et comme $\lim↙{x→+∞}1=1$, on obtient $\lim↙{x→+∞}f(x)=+∞$ (limite d'une somme).

1.b. Pour montrer que la droite $d$ d'équation $y=1$ est asymptote à $\C_f$ en $-∞$, il suffit de montrer que $\lim↙{x→-∞}f(x)=1$.
Pour lever l'indétermination en $-∞$, on développe $f(x)$.
On a $f(x)=2xe^x-2e^x+1$.
On sait que $\lim↙{x→-∞}xe^x=0$, $\lim↙{x→-∞}e^x=0$, et $\lim↙{x→-∞}1=1$.
D'où $\lim↙{x→-∞}f(x)=2×0-2×0+1=1$.
Donc $d$ est bien asymptote à $\C_f$ en $-∞$,

1.c. Pour étudier la position de $C_f$ (d'équation $y=f(x)$) par rapport à $d$ (d'équation $y=1$), on détermine le signe de $δ=f(x)-1$.
On a: $δ=f(x)-1=2(x-1)e^x+1-1=2(x-1)e^x$.
Or $2$>$0$, et $e^x$>$0$. Donc le produit $δ=2(x-1)e^x$ est du signe de $x-1$.
Si $x$<$1$, alors $δ$<$0$, et par là, $\C_f$ est en dessous de $d$.
Si $x=1$, alors $δ=0$, et $C_f$ et $d$ sont sécantes.
Si $x$>$1$, alors $δ$>$0$, et par là, $\C_f$ est au dessus de $d$.

2. On pose $f=uv+1$ avec $u=2(x-1)$ et $v=e^x$.
D'où $f\,'=u'v+uv'+0$ avec $u'=2×1=2$ et $v'=e^x$.
Donc $f\,'(x)=2e^x+2(x-1)e^x=2(1+x-1)e^x=2xe^x$.
Comme $2$ et $e^x$ sont strictement positifs, $f\,'(x)$ est du signe de $x$.
Donc $f\,'$ est strictement négative sur $]-∞;0[$, nulle en $0$, et strictement positive sur $]0;+∞[$.

3. Notons que $f(0)=2×(0-1)e^0+1=-2+1=-1$
On donne ci-dessous le tableau de variation de $f$.
On y a reporté les limites trouvées à la question 1.


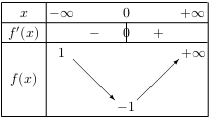
4. D'après ce tableau de variation, la fonction $f$ est continue et strictement décroissante sur $]-∞;0]$.
Or, comme $\lim↙{x→-∞}f(x)=1$ et $f(0)=-1$, on a: $\lim↙{x→-∞}f(x)\text">"0\text">"f(0)$.
Donc, d'après le théorème de la bijection, l'équation $f(x)=0$ admet une unique solution $a$ sur $]-∞;0]$.

D'après ce tableau de variation, la fonction $f$ est continue et strictement croissante sur $[0;+∞[$.
Or on a: $f(0)\text"<"0$ et $\lim↙{x→+∞}f(x)=+∞$.
Donc, d'après le théorème de la bijection, l'équation $f(x)=0$ admet une unique solution $b$ sur $[0;+∞[$.

Finalement, l'équation (1) admet exactement 2 solutions dans $\ℝ$.

5. A l'aide d'une calculatrice, on obtient:
$f(-1,68)≈1.10^{-3}$ et $f(-1,675)≈-2.10^{-3}$ et $f(-1,67)≈-5.10^{-3}$.
D'où $a≈-1,68$ (arrondie au centième).

$f(0,76)≈-0,026$ et $f(0,765)≈-0,01$ et $f(0,77)≈6,5.10^{-3}$.
D'où $b≈0,77$ (arrondie au centième).