Vecteurs, droites et plans de l'espace
A SAVOIR: le cours sur Vecteurs, droites et plans de l'espace
Exercice 1
Aucune justification n'est demandée dans cet exercice.
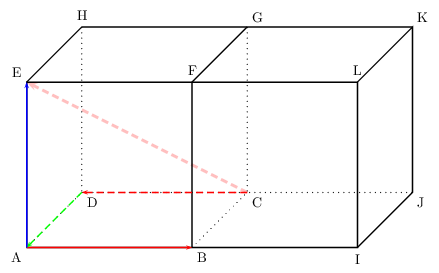
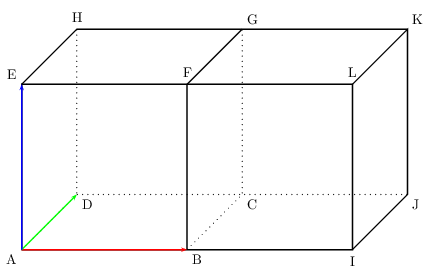
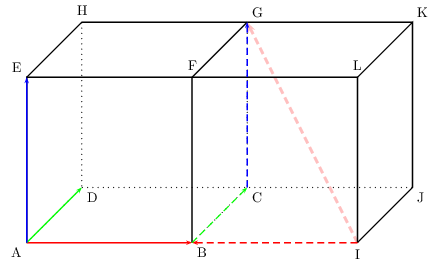
ABCDEFGH et BIJCFLKG sont deux cubes de même taille disposés côte à côte .
Reproduire la figure.
1. Construire le vecteur ${AX}↖{→}=2{AB}↖{→}+{AD}↖{→}+{AE}↖{→}$
Où est le point X?
2. Construire le vecteur ${IY}↖{→}=-2{AB}↖{→}+{AD}↖{→}+{AE}↖{→}$
Où est le point Y?
3. Ecrire le vecteur ${IG}↖{→}$ comme combinaison linéaire des vecteurs ${AB}↖{→}$, ${AD}↖{→}$ et ${AE}↖{→}$
Faire apparaître la combinaison sur le dessin.
4. Ecrire le vecteur ${CE}↖{→}$ comme combinaison linéaire des vecteurs ${AB}↖{→}$, ${AD}↖{→}$ et ${AE}↖{→}$
Faire apparaître la combinaison sur le dessin.
Solution...
Corrigé
Les justifications ci-dessous ne sont pas exigibles dans cet exercice.
On rappelle que, pour construire une somme de vecteurs, il suffit de les mettre à la queue leu leu.
1.
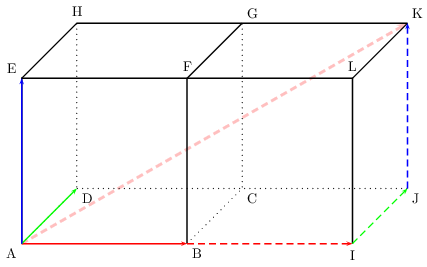
On a: ${AX}↖{→}=2{AB}↖{→}+{AD}↖{→}+{AE}↖{→}$
Or, vu les hypothèses, il est clair que:
${AB}↖{→}={BI}↖{→}$, ${AD}↖{→}={IJ}↖{→}$ et ${AE}↖{→}={JK}↖{→}$
Donc on obtient:
${AX}↖{→}={AB}↖{→}+{BI}↖{→}+{IJ}↖{→}+{JK}↖{→}$
Soit: ${AX}↖{→}= {AK}↖{→}$ (d'après la relation de Chasles).
Et par là, le point X est en K.
A retenir: l'usage de la relation de Chasles pour simplifier une somme de vecteurs.
2.
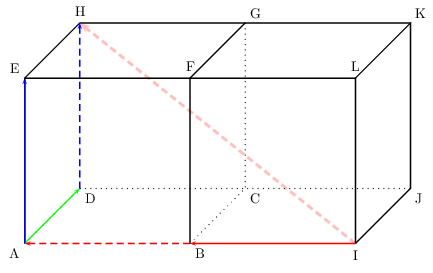
On raisonne commme précédemment.
On a: ${IY}↖{→}=-2{AB}↖{→}+{AD}↖{→}+{AE}↖{→}$
Donc, vu les hypothèses, il est clair que:
${IY}↖{→}={IB}↖{→}+{BA}↖{→}+{AD}↖{→}+{DH}↖{→}$
Soit: ${IY}↖{→}= {IH}↖{→}$ (d'après la relation de Chasles).
Et par là, le point Y est en H.
A retenir: l'usage de la relation de Chasles pour simplifier une somme de vecteurs.
3. Cette fois-ci, la relation de Chasles permet de décomposer un vecteur en une somme.
On a: ${IG}↖{→}={IB}↖{→}+{BC}↖{→}+{CG}↖{→}$ (d'après la relation de Chasles).
Soit: ${IG}↖{→}=-{AB}↖{→}+{AD}↖{→}+{AE}↖{→}$ (vu les hypothèses)
4. A nouveau, la relation de Chasles permet de décomposer un vecteur en une somme.
On a: ${CE}↖{→}={CD}↖{→}+{DA}↖{→}+{AE}↖{→}$ (d'après la relation de Chasles).
Soit: ${CE}↖{→}=-{AB}↖{→}-{AD}↖{→}+{AE}↖{→}$ (vu les hypothèses)
