Vecteurs, droites et plans de l'espace
A SAVOIR: le cours sur Vecteurs, droites et plans de l'espace
Exercice 2
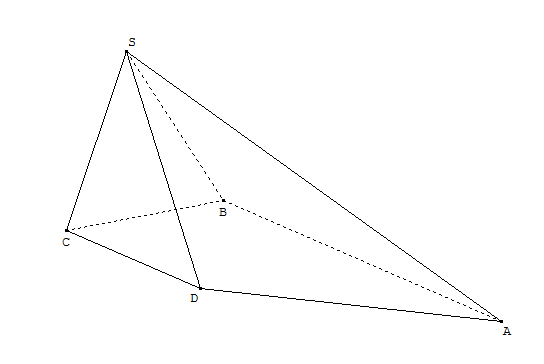
ABCDS est une pyramide non aplatie telle que,
d'une part: les droites (AB) et (CD) sont parallèles,
d'autre part: les droites (CB) et (DA) ne sont pas parallèles.
1. ${BA}↖{→}$ et ${BS}↖{→}$ ne sont pas colinéaires. Pourquoi?
Il est alors évident que ${BA}↖{→}$ et ${BS}↖{→}$ sont donc 2 vecteurs directeurs du plan (SBA).
2. Expliquer pourquoi ${BA}↖{→}$ et ${CS}↖{→}$ sont 2 vecteurs directeurs du plan (SCD).
3. 
Les plans (SBA) et (SCD) ne sont pas strictement parallèles. Pourquoi?
Les plans (SBA) et (SCD) sont sécants. Pourquoi?
4.
a. De quelle nature est l'intersection des plans (SBA) et (SCD)?
b. Soit $d_1$ cette intersection. Donner un point de $d_1$.
c. Déterminer un vecteur directeur de $d_1$.
d. Reproduire le dessin et dessiner l'intersection $d_1$ des plans (SBA) et (SCD).
5. On admettra que les plans (SBC) et (SAD) sont sécants.
a. Soit $d_2$ cette intersection. Donner un point évident de $d_2$.
b. Pourquoi les droites (CB) et (DA) sont-elles sécantes?
c. Soit F leur point d'intersection.
Pourquoi F est-il sur $d_2$?
d. Reproduire le dessin et dessiner l'intersection $d_2$ des plans (SBC) et (SAD).
Solution...
Corrigé
1. Les points A, B et S sont non alignés (sinon la pyramide serait aplatie).
Donc ${BA}↖{→}$ et ${BS}↖{→}$ ne sont pas colinéaires.
2. Il est clair que ${CD}↖{→}$ et ${CS}↖{→}$ sont 2 vecteurs directeurs du plan (SCD).
Donc ${CD}↖{→}$ et ${CS}↖{→}$ ne sont pas colinéaires et ils appartiennent à la direction de (SCD).
Or, comme les droites (AB) et (CD) sont parallèles, les vecteurs ${BA}↖{→}$ et ${CD}↖{→}$ sont colinéaires (et non nuls).
Donc ${BA}↖{→}$ et ${CS}↖{→}$ ne sont pas colinéaires et ils appartiennent à la direction de (SCD).
Donc ${BA}↖{→}$ et ${CS}↖{→}$ sont également 2 vecteurs directeurs du plan (SCD).
3. Les plans (SBA) et (SCD) ont un point commun, le point S. Donc, ils ne sont pas strictement parallèles.
Et par là, soit ils sont confondus, soit ils sont sécants.
Ils ne sont pas confondus en un plan P, car ce plan P contiendrait les points A, B, C, D et S, et la pyramide ABCDS serait aplatie.
Donc les plans (SBA) et (SCD) sont sécants.
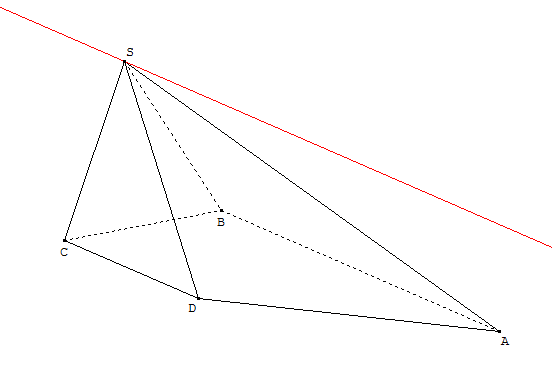
4. a. Les plans (SBA) et (SCD) sont sécants selon une droite $d_1$.
b. Le point S appartenant aux 2 plans est donc sur leur intersection $d_1$.
c. Le vecteur ${BA}↖{→}$ fait partie des vecteurs directeurs des plans (SBA) et (SCD), et donc ${BA}↖{→}$ est vecteur directeur de leur intersection $d_1$.
d. Finalement, $d_1$ est la droite passant par S de vecteur directeur ${BA}↖{→}$.
On constate qu'elle est parallèle à (AB) et à (CD)
(ce résultat résulte de l'application du "théorème du toit", hors programme)
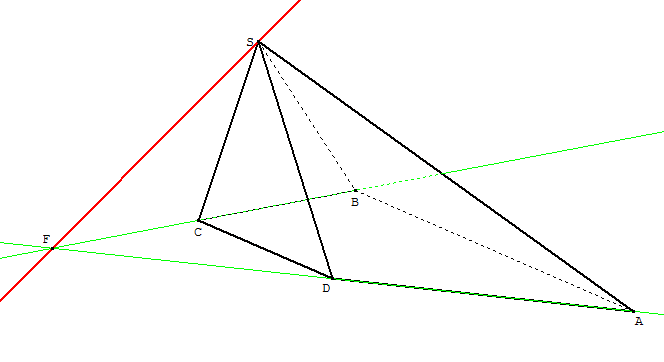
Elle est représentée en rouge dans le dessin ci-dessous.
5. a. Les plans (SBC) et (SAD) sont sécants selon une droite $d_2$ qui passe par le point S (car S appartient aux deux plans).
Reste à déterminer un second point de cette droite $d_2$ pour la tracer.
b. Les droites (CB) et (DA) ne sont pas parallèles. Or elles sont toutes deux dans le plan (ABC). Par conséquent elles sont sécantes.
c. Soit F le point d'intersection des droites (CB) et (DA).
Comme F est sur (CB), il appartient au plan (SBC).
Comme F est sur (DA), il appartient au plan (SAD).
Donc F appartient aux deux plans (SBC) et (SAD), et par là, F appartient à leur intersection, c'est à dire à la droite $d_2$.
d. Finalement, la droite $d_2$ passe donc par S et par F.
Elle est représentée en rouge dans le dessin ci-dessous.
