Vecteurs, droites et plans de l'espace
Vecteurs, droites et plans de l'espace
A SAVOIR: le cours sur Vecteurs, droites et plans de l'espace
Exercice 3
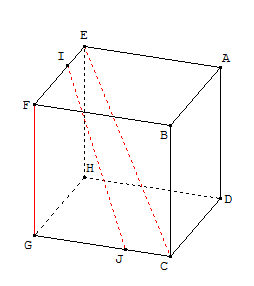
ABCDEFGH est un cube de côté non nul.
Les points I et J vérifient
${EI}↖{→}={1}/{3}{EF}↖{→}$
et ${GJ}↖{→}={2}/{3}{GC}↖{→}$.
1. Montrer que les points F, G, I, J, E et C ne sont pas coplanaires.
Peut-on en déduire que les les vecteurs ${FG}↖{→}$, ${IJ}↖{→}$ et ${EC}↖{→}$ ne sont pas coplanaires?
On va montrer ci-après que les vecteurs ${FG}↖{→}$, ${IJ}↖{→}$ et ${EC}↖{→}$ sont en réalité coplanaires, et ce par trois méthodes "différentes".
Il est vivement conseillé de connaître la relation de Chasles pour espérer répondre aux questions qui suivent...
2. Méthode 1.
a. Montrer que: ${IJ}↖{→}= {2}/{3}({EF}↖{→}+{GC}↖{→})+{FG}↖{→}$
b. En déduire que: ${IJ}↖{→}= {2}/{3}{EB}↖{→}+{FG}↖{→}$
c. Montrer finalement que: ${IJ}↖{→}= {2}/{3}{EC}↖{→}+{1}/{3}{FG}↖{→}$
d. Conclure.
3.
Méthode 2.
Ne pas utiliser ici ce qui a été prouvé dans le 2. Nous allons le démontrer autrement.
Comme ABCDEFGH est un cube de côté non nul, $({GC}↖{→}$, ${GH}↖{→}$, ${GF}↖{→})$ constitue une base de l'espace
a. Décomposer le vecteur ${EC}↖{→}$ dans la base (${GC}↖{→}$, ${GH}↖{→}$, ${GF}↖{→}$).
b. Décomposer le vecteur ${IJ}↖{→}$ dans la base (${GC}↖{→}$, ${GH}↖{→}$, ${GF}↖{→}$).
c.  Soit $a$ et $b$ deux réels.
Soit $a$ et $b$ deux réels.
On considère alors le vecteur $a. {EC}↖{→}+b. {IJ}↖{→}$.
Montrer que: $a. {EC}↖{→}+b. {IJ}↖{→}={FG}↖{→}$ $⇔$ $a=-2$ et $b=3$
d. Conclure.
4.
Méthode 3.
Ne pas utiliser ici ce qui a été prouvé dans le 2.ou le 1. Nous allons le démontrer autrement.
Cette méthode est une revisite de la méthode 2.
Comme ABCDEFGH est un cube de côté non nul, $(G,{GC}↖{→},{GH}↖{→},{GF}↖{→})$ constitue un repère de l'espace
a. Donner (sans justifier) les coordonnées des points F, G, I, J, E et C dans ce repère.
b. Donner (sans justifier) les coordonnées des vecteurs ${EC}↖{→}$, ${IJ}↖{→}$ et ${FG}↖{→}$ dans ce repère.
c. Déterminer les réels $a$ et $b$ tels que $a. {EC}↖{→}+b. {IJ}↖{→}={FG}↖{→}$
d. Conclure.
Corrigé
1. Si les points F, G, I, J, E et C étaient coplanaires, alors E appartiendrait au plan (F,G,C), et le cube serait aplati, ce qui est absurde. Donc ces points ne sont pas coplanaires.
On ne peut rien conclure quant à la coplanérité des vecteurs ${FG}↖{→}$, ${IJ}↖{→}$ et ${EC}↖{→}$.
Par contre, si les points avaient été coplanaires, alors les 3 vecteurs ${FG}↖{→}$, ${IJ}↖{→}$ et ${EC}↖{→}$, construits sur ces points, auraient été nécessairement coplanaires
Dans cet exercice, l'astuce est de décomposer les vecteurs à l'aide de la relation de Chasles.
Pour l'appliquer avec efficacité, il est conseillé de "suivre" les traits de construction, ce qui permettra une utilisation efficace des hypothèses données dans l'énoncé.
2. Méthode 1.
Préambule
ABCDEFGH est un cube , et par là: ${GC}↖{→}={FB}↖{→}$ (1)
et ${BC}↖{→}={FG}↖{→}$ (2)
Par ailleurs, on a: ${EI}↖{→}={1}/{3}{EF}↖{→}$ (3)
Enfin, comme: ${GJ}↖{→}={2}/{3}{GC}↖{→}$, on a: ${JC}↖{→}={1}/{3}{GC}↖{→}$ (4)
2.a.
On a: ${IJ}↖{→}= {IF}↖{→}+ {FG}↖{→}+ {GJ}↖{→}$ (Chasles)
Soit: ${IJ}↖{→}= {2}/{3}{EF}↖{→}+{FG}↖{→}+ {2}/{3}{GC}↖{→}$ (d'après (3) et (4))
Soit: ${IJ}↖{→}= {2}/{3}({EF}↖{→}+{GC}↖{→})+{FG}↖{→}$ c.q.f.d.
2.b. Par conséquent: ${IJ}↖{→}= {2}/{3}({EF}↖{→}+{FB}↖{→})+{FG}↖{→}$ (d'après (1))
Soit: ${IJ}↖{→}= {2}/{3}{EB}↖{→}+{FG}↖{→}$ (Chasles) c.q.f.d.
2.c. Par conséquent: ${IJ}↖{→}= {2}/{3}({EC}↖{→}-{BC}↖{→})+{FG}↖{→}$ (Chasles)
Soit: ${IJ}↖{→}= {2}/{3}({EC}↖{→}-{FG}↖{→})+{FG}↖{→}$ (d'après (2))
Soit: ${IJ}↖{→}= {2}/{3}{EC}↖{→}-{2}/{3}{FG}↖{→}+{FG}↖{→}$
Soit: ${IJ}↖{→}= {2}/{3}{EC}↖{→}+{1}/{3}{FG}↖{→}$ c.q.f.d.
2.d.
Donc il existe des nombres réels $x$ et $y$ tels que ${IJ}↖{→}= x{EC}↖{→}+y{FG}↖{→}$
Et par là, les vecteurs ${FG}↖{→}$, ${IJ}↖{→}$ et ${EC}↖{→}$ sont coplanaires.

3. Méthode 2.
Préambule
ABCDEFGH est un cube , et par là: ${EF}↖{→}=-{GH}↖{→}$ (1)
Et comme: ${EI}↖{→}={1}/{3}{EF}↖{→}$, on a: ${IF}↖{→}=-{2}/{3}{GH}↖{→}$ (2)
Enfin, on a: ${GJ}↖{→}={2}/{3}{GC}↖{→}$ (3)
3.a. On a: ${EC}↖{→}={EF}↖{→}+{FG}↖{→}+{GC}↖{→}$ (Chasles)
Soit: ${EC}↖{→}=-{GH}↖{→}-{GF}↖{→}+{GC}↖{→}$ (d'après (1))
3.b. On a: ${IJ}↖{→}={IF}↖{→}+{FG}↖{→}+{GJ}↖{→}$ (Chasles)
Soit: ${IJ}↖{→}=-{2}/{3}{GH}↖{→}-{GF}↖{→}+{2}/{3}{GC}↖{→}$ (d'après (2) et (3))
3.c. On pose: (E) $a. {EC}↖{→}+b. {IJ}↖{→}={FG}↖{→}$
On a: (E) $⇔$ $a. (-{GH}↖{→}-{GF}↖{→}+{GC}↖{→})+b. (-{2}/{3}{GH}↖{→}-{GF}↖{→}+{2}/{3}{GC}↖{→})={FG}↖{→}$ (d'après 3.a. et 3.b.)
Soit: (E) $⇔$ $(-a-{2}/{3}b){GH}↖{→}+(-a-b){GF}↖{→}+(a+{2}/{3}b){GC}↖{→}=-{GF}↖{→}$
Par unicité de la décompostion d'un vecteur dans une base (ici la base $({GC}↖{→}$, ${GH}↖{→}$, ${GF}↖{→})$), on en déduit que:
(E) $⇔$ $\{\table -a-{2}/{3}b=0;-a-b=-1;a+{2}/{3}b=0$ $⇔$ $\{\table a=-{2}/{3}b; {2}/{3}b-b=-1;a=-{2}/{3}b$
$⇔$ $\{\table a=-{2}/{3}b; b=3$ $⇔$ $\{\table a=-2; b=3$
Le système admet un couple solution $(a,b)=(-2;3)$.
3.d.
Donc il existe des nombres réels $a$ et $b$ tels que $a. {EC}↖{→}+b. {IJ}↖{→}={FG}↖{→}$
Et par là, les vecteurs ${FG}↖{→}$, ${IJ}↖{→}$ et ${EC}↖{→}$ sont coplanaires.
4. Méthode 3.
4.a. Dans le repère $(G,{GC}↖{→},{GH}↖{→},{GF}↖{→})$, on a:
$F (0;0;1)$, $G (0;0;0)$, $I(0;{2}/{3};1)$, $J({2}/{3};0;0)$, $E(0;1;1)$ et $C(1;0;0)$
3.b. On obtient alors:
${EC}↖{→}(1;-1;-1)$
${IJ}↖{→}({2}/{3};-{2}/{3};-1)$
et ${FG}↖{→}(0;0;-1)$
3.c. On pose: (E) $a. {EC}↖{→}+b. {IJ}↖{→}={FG}↖{→}$
(E) $⇔$ $\{\table a+{2}/{3}b=0;-a-{2}/{3}b=0;-a-b=-1$ $⇔$ $\{\table a=-{2}/{3}b;a=-{2}/{3}b; {2}/{3}b-b=-1$
$⇔$ $\{\table a=-{2}/{3}b; b=3$ $⇔$ $\{\table a=-2; b=3$
Le système admet un couple solution $(a,b)=(-2;3)$.
3.d.
Donc il existe des nombres réels $a$ et $b$ tels que $a. {EC}↖{→}+b. {IJ}↖{→}={FG}↖{→}$
Et par là, les vecteurs ${FG}↖{→}$, ${IJ}↖{→}$ et ${EC}↖{→}$ sont coplanaires.
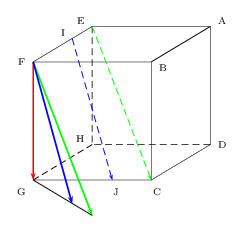
Le fait que ces 3 vecteurs appartiennent au même plan vectoriel n'est pas graphiquement évident. Pour une meilleure visualisation du problème, j'ai tracé des représentants de ces vecteurs issus du même point F.
La propriété de coplanarité saute alors aux yeux avertis...
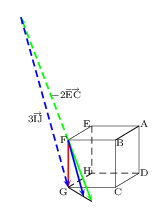
Et, pour finir, j'ai fait apparaître ci-dessous le fait que $-2 {EC}↖{→}+3 {IJ}↖{→}={FG}↖{→}$