 Intégrales
Intégrales
A SAVOIR: le cours sur les intégrales
Exercice 2
Le plan est raporté à un repère orthogonal
(unités: $1,2cm$ sur l'axe des abscisses et $0,8cm$ sur l'axe des ordonnées)
Soit $f$ de courbe représentative $C$ dans ce repère orthogonal.
$f$ est définie sur [0;4] par:
$f(x)=1$ pour $x$ dans [0;2]
$f(x)=0,5x$ pour $x$ dans ]2;4]
On admettra que $f$ est continue et positive sur [0;4].
Déterminer la valeur de $$A=∫_{0}^4 f(t)dt$$.
Quelle est l'aire de la partie hachurée (en $cm^2$)?
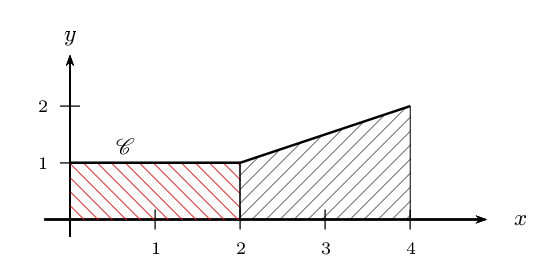
Corrigé
$f$ est continue et positive sur $[0;4]$.
Et de ce fait $A$ est l'aire du domaine $D=${$M(x;y)$/$0≤x≤4$ et $0≤y≤f(x)$}.
Cela correspond au domaine hachuré du graphique.
En appliquant la relation de Chasles, on obtient:
$$A=∫_{0}^4 f(t)dt=∫_{0}^2 f(t)dt+∫_{2}^4 f(t)dt$$
Or $$∫_{0}^2 f(t)dt$$ est l'aire du rectangle (hachuré en rouge) de côtés 2 et 1.
Donc: $$∫_{0}^2 f(t)dt=2×1=2$$
Et $$∫_{2}^4 f(t)dt$$ est l'aire du trapèze (hachuré en noir) de bases $f(2)=1$ et $f(4)=2$ et de hauteur $4-2=2$.
Donc: $$∫_{2}^4 f(t)dt={1+2}/{2}×2=3$$
Et finalement: $$A=2+3=5$$
Soit: $A=5$.
Cela correspond à l'aire du domaine hachuré (en unités d'aires).
Or 1 unité d'aire est la surface d'un rectangle de côtés 1,2 et 0,8.
Et comme $1,2×0,8=0,96$, une unité d'aire mesure $0,96 cm^2$
On calcule alors: $5×0,96=4,8$.
Finalement, l'aire de la partie hachurée est de $4,8 cm^2$.