Primitives et équations différentielles
A SAVOIR: le cours sur les primitives et équations différentielles
Exercice 1
La fonction $f$ est continue et dérivable sur $]0;5,5[ $.
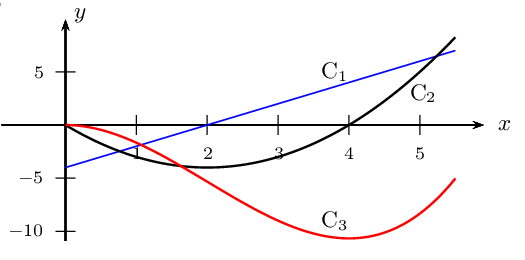
Elle est représentée ci-dessous, ainsi que sa dérivée $f'$, et l'une de ses primitives $F$.
Associer à chaque courbe sa fonction.
Corrigé
Tu peux cliquer ICI pour revoir le cours sur les primitives.
Nous allons utiliser le schéma de dérivation suivant: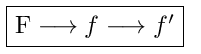 
Supposons alors que $C_1$ soit associé à la fonction $f$ ou à la fonction $F$.
Comme $C_1$ est strictement croissante, sa dérivée $f'$ (pour $f$) ou $f$ (pour $F$) serait strictement positive.
Or aucune des 2 autres courbes n'est strictement positive.
Donc $C_1$ n'est associé ni à la fonction $f$, ni à la fonction $F$.
Par élimination, il ne reste plus que $f'$.
$C_1$ est donc associé à la fonction $f'$.
Le signe de $f'$ impose le sens de variation de $f$ selon le tableau suivant:
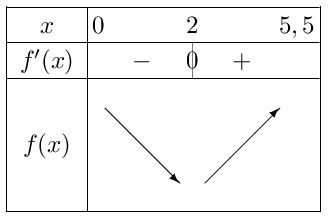
Il est alors évident que seule la courbe $C_2$ peut être associée à $f$.
Et par élimination, la courbe $C_3$ est nécessairement associée à $F$.
Nous pouvons vérifier alors le tableau de variation suivant:
