 Probabilités
Probabilités
A SAVOIR: le cours sur Sommes de variables aléatoires
Exercice 2
On jette deux tétraèdres réguliers numérotés de 1 à 4.
Soit X la variable aléatoire donnant la somme des deux résultats obtenus, et Y la variable aléatoire donnant la valeur absolue de la différence des deux résultats.
- Déterminer les lois de probabilité de X, de 2X, de Y et de Z=2X+Y.
- Déterminer les espérances $E(X)$, $E(2X)$, $E(Y)$ et $E(Z)$.
- Déterminer les variances $V(X)$, $V(2X)$, $V(Y)$ et $V(Z)$.
- Comparer $V(2X)+V(Y)$ à $V(2X+Y)$.
-
On admet que:
les variables 2X et Y sont indépendantes si et seulement si, pour tous $x$ et $y$, $p(2X=2x\,et\,Y=y)=p(2X=2x)×p(Y=y)$
Donc, s'il existe $x$ et $y$ tel que $p(2X=2x \,et\, Y=y)≠p(2X=2x)×p(Y=y)$, alors les variables 2X et Y ne sont pas indépendantes.
Les variables 2X et Y sont-elles indépendantes?
Corrigé
- $X(\Ω)=\{2;3;4;5;6;7;8\}$
Voici le tableau des sommes possibles.
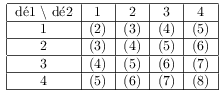
Les 16 événements étant équiprobables, on obtient facilement:

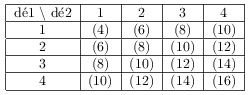
Comme il est clair que $2X=x$ $⇔$ $X={x}/{2}$, on obtient les tableaux suivants:

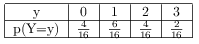
$Y(\Ω)=\{0;1;2;3\}$
Voici le tableau des différences (en valeur absolue) possibles.
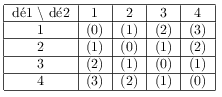
Les 16 événements étant équiprobables, on obtient facilement:
Voici le tableau des valeurs de Z possibles.
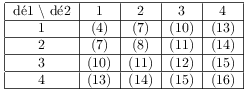
Les 16 événements étant équiprobables, on obtient facilement:

- On obtient: $E(X)={1}/{16}×2+{2}/{16}×3+{3}/{16}×4+{4}/{16}×5+{3}/{16}×6+{2}/{16}×7+{1}/{16}×8=5$
On a alors: $E(2X)=2E(X)=10$ (par linéarité de l'espérance)
Par ailleurs: $E(Y)={4}/{16}×0+{6}/{16}×1+{4}/{16}×2+{2}/{16}×3=1,25$
Enfin: $E(Z)=E(2X+Y)=2E(X)+E(Y)$ (par linéarité de l'espérance)
Soit: $E(Z)=2×5+1,25=11,25$ - On obtient: $V(X)=E(X^2)-(E(X))^2$
Soit: $V(X)={1}/{16}×2^2+{2}/{16}×3^2+{3}/{16}×4^2+{4}/{16}×5^2+{3}/{16}×6^2+{2}/{16}×7^2+{1}/{16}×8^2-5^2=27,5-25=2,5$
$V(2X)=2^2V(X)=4×2,5=10$
$V(Y)=E(Y^2)-(E(Y))^2$
Soit: $V(Y)={4}/{16}×0^2+{6}/{16}×1^2+{4}/{16}×2^2+{2}/{16}×3^2-1,25^2=2,5-1,5625=0,9375$
$V(Z)=E((Z)^2)-(E(Z))^2$
Soit: $V(Z)={1}/{16}×4^2+{2}/{16}×7^2+{1}/{16}×8^2+{2}/{16}×8^2+{2}/{16}×11^2+{1}/{16}×12^2+{2}/{16}×13^2+{2}/{16}×14^2+{2}/{16}×15^2+{1}/{16}×16^2-11,25^2$
Soit: $V(Z)=137,5-126,5625=10,9375$ - On a: $V(Z)=V(2X)+V(Y)$.
Comme $Z=2X+Y$, on constate donc que $V(2X+Y)=V(2X)+V(Y)$ -
On a, par exemple: $p(2X=4\,et\, Y=3)=0$, alors que: $p(2X=4)×p(Y=3)={1}/{16}×{2}/{16}={2}/{256}$.
Donc: $p(2X=4\,et\,Y=3)≠p(2X=4)×p(Y=3)$
Et donc les variables 2X et Y ne sont pas indépendantes!
En dépassant légèrement le programme, on admettra que: si X et Y sont 2 variables aléatoires indépendantes, alors $V(X+Y)=V(X)+V(Y)$.
Cet exercie démontre que la réciproque est fausse!