 Orthogonalité et distances dans l'espace
Orthogonalité et distances dans l'espace
A SAVOIR: le cours sur Orthogonalité et distances dans l'espace
Exercice 1
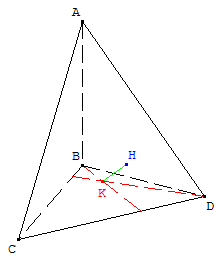
Soit ABCD un tétraèdre tel que l'arête (AB) est orthogonale au plan (BCD).
K est l'orthocentre du triangle BCD.
H est le projeté orthogonal de K sur le plan (ACD).
Attention! La perspective masque les angles droits...
1.a.
Expliquer pourquoi on a: ${AB}↖{→}.{CD}↖{→}=0$
1.b.
Expliquer pourquoi on a: ${BK}↖{→}.{CD}↖{→}=0$
1.c.
Expliquer pourquoi on a: ${KH}↖{→}.{CD}↖{→}=0$
1.d.
Montrer que: ${AH}↖{→}.{CD}↖{→}=0$
2.a.
Expliquer pourquoi on a: ${DK}↖{→}.{AB}↖{→}=0$
2.b.
Expliquer pourquoi on a: ${DK}↖{→}.{BC}↖{→}=0$
2.c.
Expliquer pourquoi on a: ${KH}↖{→}.{AC}↖{→}=0$
2.d.
Montrer que: ${DH}↖{→}.{AC}↖{→}=0$
3. Montrer que H est l'orthocentre du triangle ACD.
Corrigé
1.a. Clique ICI pour revoir quelques notions sur l'orthogonalité.
(AB) est orthogonale au plan (BCD), donc ${AB}↖{→}$ est orthogonal à tout vecteur appartenant à la direction du plan (BCD).
En particulier, ${AB}↖{→}$ est orthogonal à ${CD}↖{→}$.
Donc on a: ${AB}↖{→}.{CD}↖{→}=0$
1.b.
K est l'orthocentre du triangle BCD.
Il est donc à l'intersection des hauteurs de ce triangle.
En particulier, K est sur la hauteur de BCD issue de B.
Donc ${BK}↖{→}$ est orthogonal à ${CD}↖{→}$.
Donc on a: ${BK}↖{→}.{CD}↖{→}=0$
1.c.
H est le projeté orthogonal de K sur le plan (ACD).
Donc ${KH}↖{→}$ est orthogonal à tout vecteur appartenant à la direction du plan (ACD).
En particulier, ${KH}↖{→}$ est orthogonal à ${CD}↖{→}$.
Donc on a: ${KH}↖{→}.{CD}↖{→}=0$
1.d.
On utilise la relation de Chasles.
On obtient: ${AH}↖{→}.{CD}↖{→}=({AB}↖{→}+{BK}↖{→}+{KH}↖{→}).{CD}↖{→}$
Soit: ${AH}↖{→}.{CD}↖{→}={AB}↖{→}.{CD}↖{→}+{BK}↖{→}.{CD}↖{→}+{KH}↖{→}.{CD}↖{→}$
Et d'après les résultats précédents: ${AH}↖{→}.{CD}↖{→}=0+0+0=0$

2.a.
(AB) est orthogonale au plan (BCD), donc ${AB}↖{→}$ est orthogonal à tout vecteur appartenant à la direction du plan (BCD).
En particulier, ${AB}↖{→}$ est orthogonal à ${DK}↖{→}$.
Donc on a: ${DK}↖{→}.{AB}↖{→}=0$
2.b.
K est l'orthocentre du triangle BCD.
Il est donc à l'intersection des hauteurs de ce triangle.
En particulier, K est sur la hauteur de BCD issue de D.
Donc ${DK}↖{→}$ est orthogonal à ${BC}↖{→}$.
Donc on a: ${DK}↖{→}.{BC}↖{→}=0$
2.c.
H est le projeté orthogonal de K sur le plan (ACD).
Donc ${KH}↖{→}$ est orthogonal à tout vecteur appartenant à la direction du plan (ACD).
En particulier, ${KH}↖{→}$ est orthogonal à ${AC}↖{→}$.
Donc on a: ${KH}↖{→}.{AC}↖{→}=0$
2.d.
On utilise la relation de Chasles.
On obtient: ${DH}↖{→}.{AC}↖{→}=({DK}↖{→}+{KH}↖{→}).{AC}↖{→}$
Soit: ${DH}↖{→}.{AC}↖{→}={DK}↖{→}.{AC}↖{→}+{KH}↖{→}.{AC}↖{→}$
On utilise à nouveau la relation de Chasles.
On obtient: ${DH}↖{→}.{AC}↖{→}={DK}↖{→}.({AB}↖{→}+{BC}↖{→})+{KH}↖{→}.{AC}↖{→}$
Soit: ${DH}↖{→}.{AC}↖{→}={DK}↖{→}.{AB}↖{→}+{DK}↖{→}.{BC}↖{→}+{KH}↖{→}.{AC}↖{→}$
Et d'après les résultats précédents: ${DH}↖{→}.{AC}↖{→}=0+0+0=0$
3.
On a vu que ${AH}↖{→}.{CD}↖{→}=0$
Donc la droite (AH) est orthogonale à la droite (CD).
Donc (AH) est la hauteur de ACD issue de A.
Par ailleurs, on a vu que ${DH}↖{→}.{AC}↖{→}=0$
Donc la droite (DH) est orhtogonale à la droite (AC).
Donc (DH) est la hauteur de ACD issue de D.
Le point H est situé à l'intersection de 2 hauteurs de ACD.
Donc H est l'orthocentre du triangle ACD.