Orthogonalité et distances dans l'espace
A SAVOIR: le cours sur Orthogonalité et distances dans l'espace
Exercice 2
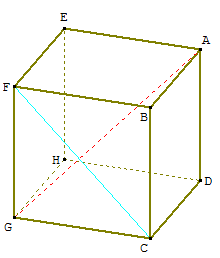
ABCDEFGH est un cube dessiné ci-contre.
On veut démontrer que les droites (AG) et (CF) sont orthogonales.
1. Méthode vectorielle.
Montrer que: ${CF}↖{→}.{AB}↖{→}=0$
Montrer que: ${CF}↖{→}.{BG}↖{→}=0$
Démontrer, en utilisant la relation de Chasles, que les vecteurs ${CF}↖{→}$ et ${AG}↖{→}$ sont orthogonaux.
Conclure.
2. Méthode analytique.
Le plan est rapporté au repère $(G,C,H,F)$.
Donner, sans justifier, les coordonnées des points G, C, H, F,et A.
Déterminer les coordonnées des vecteurs ${CF}↖{→}$ et ${AG}↖{→}$.
Conclure
Corrigé
1. Clique ICI pour revoir quelques notions sur l'orthogonalité.
ABCDEFGH est un cube , et par là:
l'arête [AB] est orthogonale au plan (BCG), et donc à toute droite qu'il contient, en particulier à la droite (CF).
et par là, on obtient: ${CF}↖{→}.{AB}↖{→}=0$ (1)
ABCDEFGH est un cube , et par là:
BCGF est un carré, et ses diagonales [CF] et [BG] sont orthogonales;
d'où l'égalité: ${CF}↖{→}.{BG}↖{→}=0$ (2)
Calculons le produit scalaire ${CF}↖{→}.{AG}↖{→}$.
${CF}↖{→}.{AG}↖{→}={CF}↖{→}.({AB}↖{→}+{BG}↖{→})$ (Chasles)
Soit: ${CF}↖{→}.{AG}↖{→}= {CF}↖{→}.{AB}↖{→}+{CF}↖{→}.{BG}↖{→}$
Soit: ${CF}↖{→}.{AG}↖{→}= 0+0$ (d'après (1) et (2))
Soit: ${CF}↖{→}.{AG}↖{→}= 0$.
Donc les vecteurs ${CF}↖{→}$ et ${AG}↖{→}$ sont orthogonaux.
Et par là, les droites (AG) et (CF) sont orthogonales.
2. Clique ICI pour revoir la formule du produit scalaire.
On a: G(0,0,0), C(1,0,0), H(0,1,0), F(0,0,1)
et: A(1,1,1).
On obtient alors:
${CF}↖{→}(-1,0,1)$
${AG}↖{→}(-1,-1,-1)$
Le repère est clairement orthonormé, et nous autorise à calculer des produits scalaires.
${CF}↖{→}.{AG}↖{→}=(-1)×(-1)+0×(-1)+1×(-1)=0$.
Donc les vecteurs ${CF}↖{→}$ et ${AG}↖{→}$ sont orthogonaux.
Et par là, les droites (AG) et (CF) sont orthogonales.