 Orthogonalité et distances dans l'espace
Orthogonalité et distances dans l'espace
A SAVOIR: le cours sur Orthogonalité et distances dans l'espace
Exercice 3
ABCD est tétraèdre régulier.
Ses faces sont des triangles équilatéraux de côté $x$.
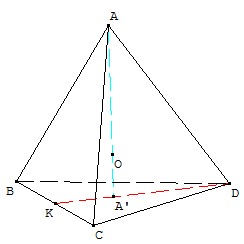
Partie 1.
On veut démontrer que les arêtes (AB) et (CD) sont orthogonales.
Montrer que: ${AB}↖{→}.{AD}↖{→}={x^2}/{2}$
Montrer que: ${AB}↖{→}.{AC}↖{→}={x^2}/{2}$
Démontrer, en utilisant la relation de Chasles, que ${AB}↖{→}.{CD}↖{→}=0$.
Conclure.
Partie 2.
Soit A' le centre de gravité de BCD.
Le point A' est défini par l'égalité: ${AA'}↖{→}={1}/{3}({AB}↖{→}+{AC}↖{→}+{AD}↖{→})$
On veut montrer que la médiane (AA') du tétraèdre est aussi une hauteur de ce tétraèdre, c'est à dire que (AA') et le plan (BCD) sont orthogonaux.
Déterminer la valeur de ${AA'}↖{→}.{BC}↖{→}$ et celle de ${AA'}↖{→}.{BD}↖{→}$.
Conclure.
Partie 3.
Soit K le milieu de [BC]. On a alors: ${KA'}↖{→}={1}/{3}{KD}↖{→}$
Montrer que $AA'=√{{2}/{3}}× x$
Partie 4.
Soit O le centre de gravité du tétraèdre.
On a alors: ${A'O}↖{→}={1}/{4}{A'A}↖{→}$
Déterminer une valeur approchée arrondie à $0,1$ degré de l'angle 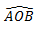
Corrigé
Partie 1. Clique ICI pour revoir quelques notions sur l'orthogonalité.
${AB}↖{→}.{AD}↖{→}=AB×AD×\cos\,$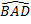
Et comme la face BAD du tétraèdre est équilatérale, on a: $\cos\,$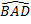 $\,=\cos \,60°={1}/{2}$
$\,=\cos \,60°={1}/{2}$
Donc on obtient: ${AB}↖{→}.{AD}↖{→}={x^2}/{2}$.
En raisonnant comme précédemment sur la face BAC, on obtient:
${AB}↖{→}.{AC}↖{→}=AB×AC×\cos\,$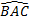 $={x^2}/{2}$.
$={x^2}/{2}$.
Calculons le produit scalaire ${AB}↖{→}.{CD}↖{→}$.
${AB}↖{→}.{CD}↖{→}={AB}↖{→}.({CA}↖{→}+{AD}↖{→})$ (Chasles)
Soit: ${AB}↖{→}.{CD}↖{→}={AB}↖{→}.{CA}↖{→}+{AB}↖{→}.{AD}↖{→}$
Soit: ${AB}↖{→}.{CD}↖{→}=-{AB}↖{→}.{AC}↖{→}+{AB}↖{→}.{AD}↖{→}$
Soit: ${AB}↖{→}.{CD}↖{→}=-{x^2}/{2}+{x^2}/{2}=0$
Et comme ${AB}↖{→}.{CD}↖{→}=0$, les vecteurs ${AB}↖{→}$ et ${CD}↖{→}$ sont orthogonaux.
Et par là, les droites (AB) et (CD) sont orthogonales.
Ce résultat se généralise sans difficulté: deux arêtes opposées d'un tétraèdre régulier sont orthogonales.

Partie 2.
On a: ${AA'}↖{→}.{BC}↖{→}={1}/{3}({AB}↖{→}+{AC}↖{→}+{AD}↖{→}).{BC}↖{→}$
${AA'}↖{→}.{BC}↖{→}={1}/{3}({AB}↖{→}.{BC}↖{→}+{AC}↖{→}.{BC}↖{→}+{AD}↖{→}.{BC}↖{→})$
Comme dans la partie 1., on obtient:
${AB}↖{→}.{BC}↖{→}=-{BA}↖{→}.{BC}↖{→}=-{x^2}/{2}$.
${AC}↖{→}.{BC}↖{→}={CA}↖{→}.{CB}↖{→}={x^2}/{2}$.
Et comme on a vu précédemment que deux arêtes opposées sont orthogonales, on a:
${AD}↖{→}.{BC}↖{→}=0$
Par conséquent, on obtient: ${AA'}↖{→}.{BC}↖{→}={1}/{3}(-{x^2}/{2}+{x^2}/{2}+0)=0$
Donc les vecteurs ${AA'}↖{→}$ et ${BC}↖{→}$ sont orthogonaux.
On montrerait de la même façon que ${AA'}↖{→}.{BD}↖{→}=0$, et par là, les vecteurs ${AA'}↖{→}$ et ${BD}↖{→}$ sont orthogonaux.
Donc finalement, ${AA'}↖{→}$ est orthogonal à ${BC}↖{→}$ et à ${BD}↖{→}$, qui sont clairement 2 vecteurs directeurs du plan (BCD).
Donc (AA') et le plan (BCD) sont orthogonaux.
Ce résultat se généralise sans difficulté: médianes et hauteurs d'un tétraèdre régulier sont confondues.

Partie 3.
On a vu que (AA') et le plan (BCD) sont orthogonaux. Donc (AA') est orthogonale à toute droite du plan (BCD), en particulier à la droite (A'K).
Donc le triangle AA'K est rectangle en A'.
Donc, par application du théorème de Pythagore, on a:
$AA'^2+A'K^2=AK^2$
Or, comme ${KA'}↖{→}={1}/{3}{KD}↖{→}$, on a: $KA'={1}/{3} KD$
De plus, comme le tétraèdre est régulier, on a: $KD=KA$
Par conséquent, on obtient finalement: $AA'^2+({1}/{3} KA)^2=AK^2$
Et par là: $AA'^2={8}/{9} KA^2$ (1)
Dans le triangle équilatéral ABC, médiane et hauteur sont confondues.
Le triangle AKC est donc rectangle en K.
Donc, par application du théorème de Pythagore, on a:
$AK^2+KC^2=AC^2$
Soit: $AK^2+({1}/{2}x)^2=x^2$
Et donc: $AK^2={3}/{4}x^2$
Et en reportant dans (1), on obtient:
$AA'^2={8}/{9}×{3}/{4}x^2$
Soit: $AA'=√{{2}/{3}}× x$ c.q.f.d.

Partie 4.
On a vu que (AA') et le plan (BCD) sont orthogonaux. Donc (AA') est orthogonale à toute droite du plan (BCD), en particulier à la droite (A'B).
Donc le projeté orthogonal du vecteur ${OB}↖{→}$ sur le vecteur ${OA}↖{→}$ est le vecteur ${OA'}↖{→}$.
Donc: ${OA}↖{→}.{OB}↖{→}={OA}↖{→}.{OA'}↖{→}$
Et comme ${A'O}↖{→}={1}/{4}{A'A}↖{→}$, on obtient:
Soit: ${OA}↖{→}.{OB}↖{→}=({3}/{4}{A'A}↖{→}).(-{1}/{4}{A'A}↖{→})$
Soit: ${OA}↖{→}.{OB}↖{→}=-{3}/{16}×AA'^2$ (a)
Par ailleurs, on sait que: ${OA}↖{→}.{OB}↖{→}=OA×OB×\cos$ 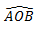
Et il est clair que: $OA=OB={3}/{4} AA'$
On a donc: ${OA}↖{→}.{OB}↖{→}={9}/{16} AA'^2×\cos$ 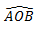 (b)
(b)
Donc finalement, par (a) et (b), on obtient:
${9}/{16} AA'^2×\cos$ 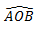 $=-{3}/{16}×AA'^2$
$=-{3}/{16}×AA'^2$
Et par là: $\cos$ 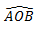 $=-{1}/{3}$
$=-{1}/{3}$
D'où: 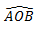 $≈$109,5 degrés (à la calculatrice)
$≈$109,5 degrés (à la calculatrice)