Orthogonalité et distances dans l'espace
Orthogonalité et distances dans l'espace
A SAVOIR: le cours sur Orthogonalité et distances dans l'espace
Exercice 4
$ P$ est un plan de l'espace, et S est un point de l'espace qui n'est pas dans $ P$.
Le projeté orthogonal de $S$ sur $ P$ est le point $A$.
$B$ est un point du plan $ P$ distinct de $A$, et $Ce1$ est le cercle du plan $ P$ de diamètre $[AB]$.
$C$ est un point du cercle $Ce1$ distinct de A et de B.
$H$ est le projeté orthogonal de $A$ sur la droite (SB).
$K$ est le projeté orthogonal de $A$ sur la droite (SC).
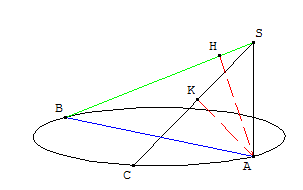
Attention! La perspective masque les angles droits...
- Montrer que: ${CB}↖{→}$ est normal au plan (ASC).
- Montrer que: ${AK}↖{→}$ est normal au plan (BSC).
- En utilisant la relation de Chasles et le résultat de la question 2., montrer que: ${SB}↖{→}.{HK}↖{→}=0$
- Pourquoi a-t-on l'égalité: ${AK}↖{→}.{HK}↖{→}=0$
- Montrer que le point K est sur le cercle $Ce2$ de diamètre $[AH]$ contenu dans le plan perpendiculaire à (SB) et passant par H.
- Montrer que lorsque le point K lorsque C décrit tout le cercle $Ce1$, alors K est sur le cercle $Ce2$.
Corrigé
- Le plan (ASC) admet pour vecteurs directeurs ${AC}↖{→}$ et ${AS}↖{→}$.
Or, comme $C$ est sur le cercle $Ce1$ de diamètre $[AB]$, on a: ${CB}↖{→}.{AC}↖{→}=0$ (a)
Et comme $A$ est le projeté orthogonal de $S$ sur $ P$, ${AS}↖{→}$ est orthogonal à tout vecteur appartenant à la direction du plan $ P$.
Et comme $B$ et $C$ sont tous les deux dans $ P$, , on obtient: ${CB}↖{→}.{AS}↖{→}=0$ (b)
Par conséquent, d'après (a) et (b), ${CB}↖{→}$ est orthogonal à deux vecteurs directeurs du plan (ASC).
Donc ${CB}↖{→}$ est normal au plan (ASC). - Le plan (BSC) admet pour vecteurs directeurs ${CB}↖{→}$ et ${CS}↖{→}$.
Or ${CB}↖{→}$ est normal au plan (ASC) (d'après le 1.).
Donc il est orthogonal à tout vecteur appartenant à la direction du plan (ASC), en particulier, au vecteur ${AK}↖{→}$ (qui appartient évidemment à la direction du plan (ASC).
On a donc : ${AK}↖{→}.{CB}↖{→}=0$ (c)
Par ailleurs, comme $K$ est le projeté orthogonal de $A$ sur la droite (SC), on a: ${AK}↖{→}.{CS}↖{→}=0$ (d)
Par conséquent, d'après (c) et (d), ${AK}↖{→}$ est orthogonal à deux vecteurs directeurs du plan (BSC).
Donc ${AK}↖{→}$ est normal au plan (BSC). - On a: ${SB}↖{→}.{HK}↖{→}={SB}↖{→}.({HA}↖{→}+{AK}↖{→})$ (Chasles)
Soit: ${SB}↖{→}.{HK}↖{→}={SB}↖{→}.{HA}↖{→}+{SB}↖{→}.{AK}↖{→}$
Or, comme $H$ est le projeté orthogonal de $A$ sur la droite (SB), on a: ${SB}↖{→}.{HA}↖{→}=0$
Et comme ${AK}↖{→}$ est normal au plan (BSC) (d'après le 2.), on a: ${SB}↖{→}.{AK}↖{→}=0$.
Par conséquent, on obtient: ${SB}↖{→}.{HK}↖{→}=0+0=0$ c.q.f.d.
- Comme ${AK}↖{→}$ est normal au plan (BSC) (d'après le 2.), il est orthogonal à tout vecteur appartenant à la direction du plan (BSC), en particulier, au vecteur ${HK}↖{→}$ (qui appartient évidemment à la direction du plan (BSC).
Donc on a bien: ${AK}↖{→}.{HK}↖{→}=0$
- Comme ${SB}↖{→}.{HK}↖{→}=0$ (d'après le 3.), le point K est dans le plan perpendiculaire à (SB) et passant par H.
Et comme ${AK}↖{→}.{HK}↖{→}=0$, ce point K est sur le cercle $Ce2$ de diamètre $[AH]$ contenu dans le plan perpendiculaire à (SB) et passant par H. c.q.f.d.
- On rappelle que les hypothèses précisent que le point $C$ est un point du cercle $Ce1$ distinct de A et de B.
On vient donc de montrer que, si le point C est dans le cercle $Ce1$ privé des points $A$ et $B$, alors le point K est sur le cercle $Ce2$.
Examinons le cas où C est en A.
Le point K est alors en A, et le point K est donc bien sur le cercle $Ce2$.
Examinons le cas où C est en B.
Le point K est alors en H, et le point K est donc bien sur le cercle $Ce2$.
Par conséquent, lorsque C décrit tout le cercle $Ce1$, K est sur le cercle $Ce2$.
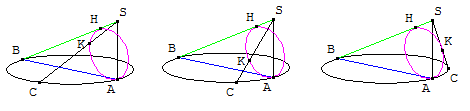
Voici quelques figures qui précisent l'idée précédente.