Orthogonalité et distances dans l'espace
A SAVOIR: le cours sur Orthogonalité et distances dans l'espace
Exercice 5
Soient A et B deux points distincts de l'espace, et soit I le milieu de [AB].
Soit P le plan passant par I et de vecteur normal ${AB}↖{→}$.
Le plan P s'appelle plan médiateur du segment [AB].
- Soit M un point quelconque de P.
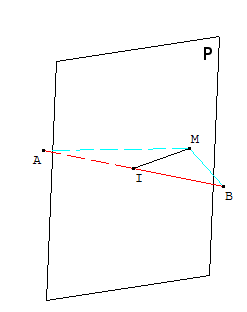
Si M est en I, alors il est évident que $AM=MB$.
Supposons que M soit distinct de I. On peut alors considérer le plan (ABM).
Montrer que M appartient à la médiatrice de [AB] dans le plan (ABM).
Qu'en déduire concernant AM et MB? - Démontrons la réciproque.
Supposons cette fois que M est un point de l'espace tel que $AM=MB$.
Si M est en I, alors il est évident que M est sur P.
Supposons que M soit distinct de I. On peut alors considérer le plan (ABM) si besoin.
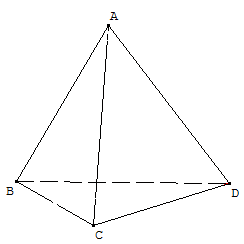
Montrer que M appartient à P. - Reprenons le tétraèdre régulier ABCD de l'exercice 3. Montrer en utilisant un plan médiateur que les arêtes (AB) et (CD) sont orthogonales.
Corrigé
- Soit M un point quelconque de P.
Comme I est dans P, ${MI}↖{→}$ est un vecteur appartenant à la direction de P.
Et comme le plan P a pour vecteur normal ${AB}↖{→}$, les vecteurs ${AB}↖{→}$ et ${MI}↖{→}$ sont orthogonaux.
Par conséquent, dans le plan (ABM), la droite (MI) est perpendiculaire à [AB].
Et comme elle passe par son milieu I, c'est la médiatrice de [AB] dans le plan (ABM).
Et donc $AM=MB$. - M est un point de l'espace distinct de I tel que $AM=MB$.
Donc, dans le plan (ABM), M appartient à la médiatrice de [AB].
Or I, milieu de [AB], est clairement sur la médiatrice de[AB].
Donc la médiatrice de [AB] est la droite (MI).
Et par là, les vecteurs ${AB}↖{→}$ et ${MI}↖{→}$ sont orthogonaux.
Or P est le plan passant par I et de vecteur normal ${AB}↖{→}$.
Donc M appartient à P. - Reprenons le tétraèdre régulier ABCD de l'exercice 3.
Le tétraèdre ABCD est régulier, donc: $DA=CA$, et donc A appartient au plan médiateur de [CD].
De même, $DB=CB$, et donc B appartient au plan médiateur de [CD].
Donc ${AB}↖{→}$ appartient à la direction de ce plan médiateur.
Or ce plan médiateur a pour vecteur normal ${CD}↖{→}$.
Donc ${CD}↖{→}$ est orthogonal à tout vecteur de la direction de ce plan médiateur, en particulier à ${AB}↖{→}$.
Donc les arêtes (AB) et (CD) sont orthogonales.