 Orthogonalité et distances dans l'espace
Orthogonalité et distances dans l'espace
A SAVOIR: le cours sur Orthogonalité et distances dans l'espace
Exercice 6
L'espace est rapporté au repère orthonormal (O,I,J,K).
On considère les points $M(0,5;0;0,5)$, $N(0;1;0,5)$, $P(1;1;0)$ et $A(1;1;1)$.
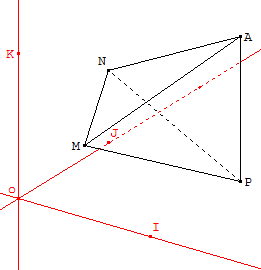
- Soit ${n}↖{→}(a;1;b)$ un vecteur orthogonal à ${MP}↖{→}$ et ${MN}↖{→}$.
Déterminer les valeurs de $a$ et $b$. - Montrer que le point $R(x;y;z)$ appartient au plan $(MNP)$ si et seulement si $2x+y+4z-3=0$
- Expliquer pourquoi le point $S(x;y;z)$ appartient à la droite $d$ passant par A et orthogonale au plan $(MNP)$ si et seulement si il existe un réel $t$ tel que $\{\table x=1+2t; y=1+t; z=1+4t$
- Déterminer les coordonnées du point H, projeté orthogonal de A sur $(MNP)$.
Placer le point H sur le dessin. - On admet que l'aire du triangle MNP vaut environ 0,57 unités d'aires. Calculer le volume du tétraèdre AMNP.
Corrigé
- On obtient facilement: ${MP}↖{→}(0.5;1;-0.5)$ et ${MN}↖{→}(-0.5;1;0)$
Le repère étant orthonormé, on obtient:
${MP}↖{→}.{n}↖{→}=0.5a+1-0.5b$ et ${MN}↖{→}.{n}↖{→}=-0.5a+1$.
Par conséquent:${n}↖{→}(a;1;b)$ est orthogonal à ${MP}↖{→}$ et ${MN}↖{→}$
$ ⇔$ $\{\table 0.5a+1-0.5b=0; -0.5a+1=0$ $⇔$ $\{\table 0.5a+1-0.5b=0; a=2$
$⇔$ $\{\table b=4; a=2$
Et par là, on obtient: ${n}↖{→}(2;1;4)$ - ${n}↖{→}$ un vecteur orthogonal à deux vecteurs ${MP}↖{→}$ et ${MN}↖{→}$ non colinéaires (car leurs coordonnées ne sont pas proportionnelles).
Or ces deux vecteurs appartiennent à la direction du plan $(MNP)$.
Donc ${n}↖{→}$ est un vecteur normal au plan $(MNP)$.
Par conséquent, le point $R(x;y;z)$ appartient au plan $(MNP)$ si et seulement si ${MR}↖{→}.{n}↖{→}=0$
Or on obtient facilement: ${MR}↖{→}(x-0.5;y;z-0.5)$, et on sait que: ${n}↖{→}(2;1;4)$
Donc: $R(x;y;z)$ $∈$ $(MNP)$ $ ⇔$ $ 2(x-0.5)+1y+4(z-0.5)=0$ $ ⇔$ $2x-1+y+4z-2=0$
Et finalement: $R(x;y;z)$ $∈$ $(MNP)$ $ ⇔$ $2x+y+4z-3=0$
Pour information, cette égalité est une "équation cartésienne" du plan $(MNP)$ - Comme ${n}↖{→}$ est un vecteur normal au plan $(MNP)$, le point $S(x;y;z)$ appartient à la droite $d$ passant par A et orthogonale au plan $(MNP)$ si et seulement si ${AS}↖{→}$ et ${n}↖{→}$ sont colinéaires.
Donc $S(x;y;z)$ $∈$ $d$ $ ⇔$ il existe un réel $t$ tel que ${AS}↖{→}=t{n}↖{→}$
Et comme on a: ${AS}↖{→}(x-1;y-1;z-1)$ et ${n}↖{→}(2;1;4)$, on obtient:
$S(x;y;z)$ $∈$ $d$ $ ⇔$ il existe un réel $t$ tel que $\{\table x-1=2t; y-1=t; z-1=4t$
Soit: $S(x;y;z)$ $∈$ $d$ $ ⇔$ il existe un réel $t$ tel que $\{\table x=1+2t; y=1+t; z=1+4t$
Pour information, ce système donne une "représentation paramétrique" de la droite $d$. - Comme la droite $d$ passe par A et est orthogonale au plan $(MNP)$, le point H, projeté orthogonal de A sur $(MNP)$, est situé à l'intersection de $d$ et de $(MNP)$.
Par conséquent, ses coordonnées $(x;y;z)$ vérifient l'équation cartésienne du plan et la représentation paramétrique de la droite.
Par substitution, on obtient alors:
(E) $2(1+2t)+(1+t)+4(1+4t)-3=0$
Or: (E) $ ⇔$ $2+4t+1+t+4+16t-3=0$ $ ⇔$ $t=-{4}/{21}$
Donc les coordonnées de H sont: $\{\table x=1+2×(-{4}/{21})={13}/{21}≈0.6; y=1+(-{4}/{21})={17}/{21}≈0.8; z=1+4×(-{4}/{21})={5}/{21}≈0.2$
Donc: $H({13}/{21};{17}/{21};{5}/{21})$
On a placé le point H sur le dessin ci-dessous.
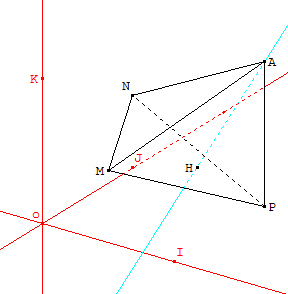
- Le volume d'un tétraèdre est donné par la formule: ${b×h}/{3}$,
où $b$ est l'aire d'une base et $h$ la longueur de la hauteur correspondante.
Ici, la base sera la face MNP et la hauteur sera évidemment [AH].
On a: $b≈0,57$.
Or, on obtient: ${AH}↖{→}(-{8}/{21};-{4}/{21};-{16}/{21})$,
et donc: $AH=√{(-{8}/{21})^2+(-{4}/{21})^2+(-{16}/{21})^2}={4√{21}/{21}≈0,87$
Et donc le volume cherché est environ égal à:
${0,57×0,87}/{3}≈0,17$