Corrigé

La notation $a=b$ $[x]$, où x est un réel, est équivalente à: $a=b+kx$ où $k∈\ℤ$.
$a=b$ $[x]$ se dit "$a$ égale $b$ modulo $x$"

La résolution d'une équation trigonométrique utilise souvent
soit l'équivalence $\sin a=\sin b$ $⇔$ $a=b$ $[2π]$ ou $a=π-b$ $[2π]$
soit l'équivalence $\cos a=\cos b$ $⇔$ $a=b$ $[2π]$ ou $a=-b$ $[2π]$.

1. On résout sur $\ℝ$.
(1)$⇔$ $2\sin(3x)-1=0$ $⇔$ $\sin(3x)={1}/{2}$ $⇔$ $\sin(3x)=\sin{π}/{6}$
Soit: (1)$⇔$ $3x={π}/{6}+2kπ$    ou    $3x=π-{π}/{6}+2kπ$    avec $k∈\ℤ$
Soit: (1)$⇔$ $x={π}/{18}+k{2π}/{3}$    ou    $x={5π}/{18}+k{2π}/{3}$    avec $k∈\ℤ$

Donc $\S_1=\{{π}/{18}$ $[{2π}/{3}]$ ; ${5π}/{18}$ $[{2π}/{3}]\}$.

2. On résout tout d'abord sur $\ℝ$.
(2) $⇔$ $\cos^2(2x)={2}/{4}$ $⇔$ $\cos(2x)={√{2}}/{2}$    ou    $\cos(2x)=-{√{2}}/{2}$
Soit: (2) $⇔$ $\cos(2x)=\cos{π}/{4}$    ou    $\cos(2x)=\cos(π-{π}/{4})$
Soit: (2) $⇔$ $\cos(2x)=\cos{π}/{4}$    ou    $\cos(2x)=\cos({3π}/{4})$

On résout tout d'abord la première équation: $\cos(2x)=\cos{π}/{4}$    (a)
(a) $⇔$ $2x={π}/{4}+2kπ$    ou    $2x=-{π}/{4}+2kπ$    avec $k∈\ℤ$
Soit: (a) $⇔$ $x={π}/{8}+kπ$    ou    $x=-{π}/{8}+kπ$    avec $k∈\ℤ$
Mais seules les solutions dans $]-π;π]$ sont demandées.
Il s'agit de: ${π}/{8}+0×π={π}/{8}$,    ${π}/{8}-1×π=-{7π}/{8}$,    $-{π}/{8}+0×π=-{π}/{8}$    et    $-{π}/{8}+1×π={7π}/{8}$

On résout ensuite la seconde équation: $\cos(2x)=\cos{3π}/{4}$    (b)
(b) $⇔$ $2x={3π}/{4}+2kπ$    ou    $2x=-{3π}/{4}+2kπ$    avec $k∈\ℤ$
Soit: (b) $⇔$ $x={3π}/{8}+kπ$    ou    $x=-{3π}/{8}+kπ$    avec $k∈\ℤ$
Mais seules les solutions dans $]-π;π]$ sont demandées.
Il s'agit de: ${3π}/{8}+0×π={3π}/{8}$,    ${3π}/{8}-1×π=-{5π}/{8}$,    $-{3π}/{8}+0×π=-{3π}/{8}$    et    $-{3π}/{8}+1×π={5π}/{8}$

Finalement, on obtient donc: $\S_2=\{-{7π}/{8};-{5π}/{8};-{3π}/{8};-{π}/{8};{π}/{8};{3π}/{8};{5π}/{8};{7π}/{8}\}$.

Autre méthode:
(2) $⇔$ $2\cos^2(2x)-1=0$ $⇔$ $\cos(4x)=0$
Soit: (2) $⇔$ $\cos(4x)=\cos{π}/{2}$    ou    $\cos(4x)=\cos(-{π}/{2})$
Soit: (2) $⇔$ $4x={π}/{2}+2kπ$    ou    $4x=-{π}/{2}+2kπ$    avec $k∈\ℤ$
Soit: (2) $⇔$ $x={π}/{8}+k{π}/{2}$    ou    $x=-{π}/{8}+k{π}/{2}$    avec $k∈\ℤ$
On retrouve alors les mêmes solutions dans $]-π;π]$ qu'avec la première méthode.



La résolution d'une inéquation trigonométrique nécessite souvent la résolution de l'équation trigonométrique associée, puis d'un raisonnement reposant sur le cercle trigonométrique.
3. (3) $⇔$ $2\sin x-√{3}$<$0$ $⇔$ $\sin x$<${√{3}}/{2}$

On résout l'équation trigonométrique associée.
$\sin x= {√{3}}/{2}$ $⇔$ $\sin x=\sin{π}/{3}$ $⇔$ $x={π}/{3}$ $[2π]$ ou $x=π-{π}/{3}$ $[2π]$.
Donc, sur $]-π;π]$, on a: $\sin(x)={√{3}}/{2}$ $⇔$ $x={π}/{3}$ ou $x={2π}/{3}$.

On revient alors à l'inéquation.
Par lecture du cercle trigonométrique, on obtient:
(3) $⇔$ $-π$<$x$<${π}/{3}$    ou    ${2π}/{3}$<$x≤π$.


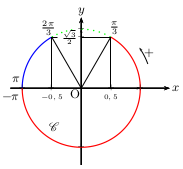
Donc $\S_3=]-π;{π}/{3}[∪]{2π}/{3};π]$.

4.a. On calcule: $({1}/{2})^2+({√{3}-1}/{2})({1}/{2})-{√{3}}/{4}={1}/{4}+{√{3}-1}/{4}-{√{3}}/{4}=0$.
Donc ${1}/{2}$ est racine du trinôme $X^2+({√{3}-1}/{2})X-{√{3}}/{4}$.

4.b. On rappelle que, si le trinôme $ax^2+bx+c$ admet pour racines réelles (éventuellement doubles) $x_1$ et $x_2$, alors il se factorise sous la forme: $a(x-x_1)(x-x_2)$.
Or ici, le trinôme a au moins une racine réelle.
Il est donc factorisable sous cette forme, et on a, pour tout $X$ réel, l'égalité: $X^2+({√{3}-1}/{2})X-{√{3}}/{4}=1(X-x_1)(X-{1}/{2})$.
On développe le membre de gauche.
On obtient alors l'égalité, vérifiée pour tout $X$ réel:
$X^2+({√{3}-1}/{2})X-{√{3}}/{4}=X^2+(-x_1-{1}/{2})X+{x_1}/{2}$.
Par identification, on obtient alors:     $1=1$    et    ${√{3}-1}/{2}=-x_1-{1}/{2}$    et    $-{√{3}}/{4}={x_1}/{2}$.
D'où: $-{√{3}}/{2}=x_1$ dans les deux dernières équations (ce qui est rassurant).
La seconde racine du trinôme est donc $-{√{3}}/{2}$.

4.c. (4) $⇔$ $\cos^2x+({√{3}-1}/{2})\cos x-{√{3}}/{4}≥0$

On pose alors: $X=\cos x$, et on résout: $X^2+({√{3}-1}/{2})X-{√{3}}/{4}≥0$.
Le membre de gauche est le trinôme précédent, qui a 2 racines: $-{√{3}}/{2}$ et ${1}/{2}$, et dont le coefficient dominant vaut 1.
Comme le coefficient dominant du trinôme est positif, ce trinôme est positif ou nul à l'extérieur de ses racines, et par là, sur $]-\∞;-{√{3}}/{2}]∪[{1}/{2};+\∞[$.
On a donc: $X^2+({√{3}-1}/{2})X-{√{3}}/{4}≥0$ $⇔$ $\X≤-{√{3}}/{2}$ ou $X≥{1}/{2}$.

Or, comme on avait posé $X=\cos x$, on revient alors à l'inéquation d'origine, et on obtient:
(4) $⇔$ $\cos x≤-{√{3}}/{2}$ ou $\cos x≥{1}/{2}$.
Soit (a) l'inéquation $\cos x≤-{√{3}}/{2}$ et (b) l'inéquation $\cos x≥{1}/{2}$.

On résout l'équation trigonométrique associée à (a).
$\cos x=-{√{3}}/{2}$ $⇔$ $\cos x=\cos (π-{π}/{6})$ $⇔$ $\cos x=\cos ({5π}/{6})$
Soit: $\cos x=-{√{3}}/{2}$ $⇔$ $x={5π}/{6}$ $[2π]$    ou     $x=-{5π}/{6}$ $[2π]$
Et comme on raisonne sur $]-π;π]$, on obtient:    $x={5π}/{6}$     ou     $x=-{5π}/{6}$
On revient alors à l'inéquation (a): $\cos x≤-{√{3}}/{2}$.
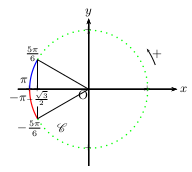
Par lecture du cercle trigonométrique, on obtient:
(a) $⇔$ $-π$<$x≤-{5π}/{6}$    ou    ${5π}/{6}≤x≤π$.


On résout l'équation trigonométrique associée à (b).
$\cos x={1}/{2}$ $⇔$ $\cos x=\cos ({π}/{3})$
Soit: $\cos x={1}/{2}$ $⇔$ $x={π}/{3}$ $[2π]$    ou     $x=-{π}/{3}$ $[2π]$
Et comme on raisonne sur $]-π;π]$, on obtient:    $x={π}/{3}$     ou     $x=-{π}/{3}$
On revient alors à l'inéquation (b): $\cos x≥{1}/{2}$.
Par lecture du cercle trigonométrique, on obtient:
(b) $⇔$ $-{π}/{3}≤x≤{π}/{3}$


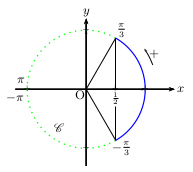
Finalement: $\S_4=]-π;-{5π}/{6}]∪[-{π}/{3};{π}/{3}]∪[{5π}/{6};π]$.