Fonctions sinus et cosinus
A SAVOIR: le cours sur sinus et cosinus
Exercice 2
Soit $f$ définie sur $[0;π]$ par $f(x)=\sin(2x)-x$.
Soit $\C_f$ sa courbe représentative.
1. Déterminer la valeur exacte de $f(0)$, $f({π}/{6})$, $f({5π}/{6})$ et $f(π)$.
2.a. Montrer que $f\,'(x)=2×\cos(2x)-1$
2.b. On admet que, pour tout $x$, on a: $\cos(2x)=2\cos^2 x-1$.
Montrer que $f\,'(x)=4\cos^2 x-3$.
3.a. Résoudre l'inéquation: $4X^2-3≥0$.
3.b. Résoudre sur $[0;π]$ l'inéquation $4\cos^2 x-3≥0$, puis déterminer le sens de variation de $f$ sur $[0;π]$.
4. 
Retrouvons le sens de variation de $f$ sur $[0;π]$ par une autre méthode (non exigible).
Résoudre sur $[0;π]$ l'inéquation $2×\cos(2x)-1≥0$, puis retrouver le sens de variation de $f$ sur $[0;π]$.
5. Déterminer une équation de la tangente $t$ à $\C_f$ en ${π}/{2}$.
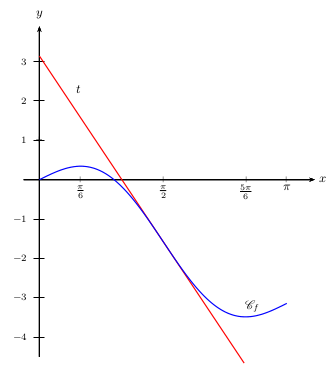
6. Représenter graphiquement $\C_f$ et $t$.
Corrigé
1. $f(0)=0$
$f({π}/{6})=\sin({π}/{3})-{π}/{6}={√{3}}/{2}-{π}/{6}$
$f({5π}/{6})=\sin({5π}/{3})-{5π}/{6}=\sin(-{π}/{3})-{5π}/{6}=-{√{3}}/{2}-{5π}/{6}$
$f(π)=\sin(2π)-π=-π$
2.a. On pose $f=g(2x+0)-x$ avec $g(y)=\sin y$.
Donc $f\,'=2g'(2x+0)-1$ avec $g'(y)=\cos y$.
Et par là: $f\,'(x)=2×\cos(2x)-1$.
2.b. On a: $f\,'(x)=2×\cos(2x)-1$.
Or: $\cos(2x)=2\cos^2 x-1$
Donc $f\,'(x)=2(2\cos^2 x-1)-1=4\cos^2 x-2-1$.
Soit: $f\,'(x)=4\cos^2 x-3$
3.a. On a: $4X^2-3≥0$ $⇔$ $X^2≥{3}/{4}$ $⇔$ $X≤-{√{3}}/{2}$ ou $X≥{√{3}}/{2}$
3.b. On résout sur $[0;π]$ l'inéquation : $4\cos^2 x-3≥0$ (1)
Or, si on pose $X=\cos x$, l'inéquation devient: $4X^2-3≥0$.
Et cette inéquation a été résolue au 2.b..
Par conséquent:
(1) $⇔$ $\cos x≤-{√{3}}/{2}$ ou $\cos x≥{√{3}}/{2}$
On résout les équations trigonométriques associées.
$\cos x= -{√{3}}/{2}$ $⇔$ $\cos x=\cos(π-{π}/{6})=\cos{5π}/{6}$ $⇔$ $x={5π}/{6} +2kπ$ ($k ∈ ℤ$) ou $x=-{5π}/{6}+2k'π$ ($k ∈ ℤ$)
Soit: $\cos x= -{√{3}}/{2}$ $⇔$ $x={5π}/{6}$ $[2π]$ ou $x=-{5π}/{6}$ $[2π]$.
Donc, sur $[0;π]$, on a: $\cos x= -{√{3}}/{2}$ $⇔$ $x={5π}/{6}$.
On revient alors à l'inéquation $\cos x≤-{√{3}}/{2}$.
Par lecture du cercle trigonométrique, on obtient:
$\cos x≤-{√{3}}/{2}$ $⇔$ ${5π}/{6}$<$x≤π$ (on rappelle que $x$ est cherché dans $[0;π]$)
Cela correspond à l'arc bleu ci-dessous.
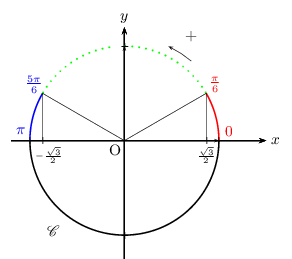
On procède de même avec la seconde inéquation.
$\cos x= {√{3}}/{2}$ $⇔$ $\cos x=\cos({π}/{6})$ $⇔$ $x={π}/{6}$ $[2π]$ ou $x=-{π}/{6}$ $[2π]$.
Donc, sur $[0;π]$, on a: $\cos x= {√{3}}/{2}$ $⇔$ $x={π}/{6}$.
On revient alors à l'inéquation $\cos x≥{√{3}}/{2}$.
Par lecture du cercle trigonométrique, on obtient:
$\cos x≥{√{3}}/{2}$ $⇔$ $0≤x≤{π}/{6}$ (on rappelle que $x$ est cherché dans $[0;π]$)
Cela correspond à l'arc rouge ci-dessus.
On vient de trouver pour quels $x$ la dérivée $f\,'(x)$ est positive.
D'où le tableau de signes de $f\,'$ et le tableau de variation de $f$:
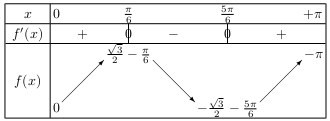
4. On résout sur $[0;π]$ l'inéquation : $2×\cos(2x)-1≥0$ (2)
On a: (2) $⇔$ $\cos(2x)≥{1}/{2}$
On résout l'équation trigonométrique associée.
$\cos(2x)={1}/{2}$ $⇔$ $\cos(2x)=\cos({π}/{3})$
Soit: $\cos(2x)={1}/{2}$ $⇔$ $⇔$ $2x={π}/{3}+2kπ$ ($k ∈ ℤ$) ou $2x=-{π}/{3}+2k'π$ ($k' ∈ ℤ$)
Soit: $\cos(2x)={1}/{2}$ $⇔$ $x={π}/{6}+kπ$ ($k ∈ ℤ$) ou $x=-{π}/{6}+k'π$ ($k' ∈ ℤ$)
Donc, sur $[0;π]$, on a: $\cos(2x)={1}/{2}$ $⇔$ $x={π}/{6}$ ou $x={5π}/{6}$
On revient alors à l'inéquation (2): $\cos(2x)≥{1}/{2}$.
On résout sur $[0;π]$. Les intervalles à examiner sont donc: $[0;{π}/{6}]$, $[{π}/{6};{5π}/{6}]$ et $[{5π}/{6};π]$.
Or, par lecture du cercle trigonométrique, on obtient:
$0≤x≤{π}/{6}$ $⇒$ $0≤2x≤{π}/{3}$ $⇒$ $\cos(2x)≥{1}/{2}$.
${π}/{6}≤x≤{5π}/{6}$ $⇒$ ${π}/{3}≤2x≤{5π}/{3}$ $⇒$ $\cos(2x)≤{1}/{2}$.
${5π}/{6}≤x≤π$ $⇒$ ${5π}/{3}≤2x≤2π$ $⇒$ $\cos(2x)≥{1}/{2}$.
On vient donc de trouver pour quels $x$ la dérivée $f\,'(x)$ est positive.
D'où le tableau de signes de $f\,'$ et le tableau de variation de $f$:
5. $f({π}/{2})=\sin{π}-{π}/{2}=-{π}/{2}$
$f\,'({π}/{2})=4\cos^2({π}/{2})-3=-3$
Donc $t$ admet pour équation: $y=-{π}/{2}+(-3)(x-{π}/{2})$
Soit: $y=-3x+π$.
6. Voici les tracés demandés:
