Corrigé

1. $f$ est un trinôme avec $a=1$, $b={2}/{3}$, $c=0$, et par là: ${-b}/{2a}=-{1}/{3}$.
Comme $a\text">"0$, on obtient le tableau de variation suivant:


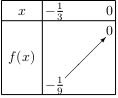
2. Clique ICI pour revoir l'essentiel sur la démonstration par récurrence.
Soit $P_n$ la propriété: $0\text">"u_n\text">"-{1}/{3}$.
Démontrons par récurrence que, pour tout naturel $n$ , la propriété $P_n$ est vraie.
Initialisation: $u_0=-{1}/{6}$. On a bien $0\text">"u_0\text">"-{1}/{3}$. Donc $P_{0}$ est vraie.
Hérédité:
Soit $n$ un entier naturel, supposons que $P_n$ soit vraie.
$0\text">"u_n\text">"-{1}/{3}$.
Donc, comme $f$ est strictement croissante sur $[-{1}/{3};0]$, on a: $f(0)\text">"f(u_n)\text">"f(-{1}/{3})$.
Soit: $0\text">"u_{n+1}\text">"-{1}/{9}$.
Et par là: $0\text">"u_{n+1}\text">"-{1}/{3}$.
Donc $P_{n+1}$ est vraie.
Conclusion: pour tout naturel $n$, $0\text">"u_n\text">"-{1}/{3}$.

3. Pour démontrer que la suite $(u_n)$ est strictement croissante, il suffit de démontrer que, pour tout naturel $n$, $u_n\text"<"u_{n+1}$ .
Soit $Q_n$ la propriété: $u_n\text"<"u_{n+1}$.

Méthode 1: Démontrons par récurrence que, pour tout naturel $n$ , la propriété $Q_n$ est vraie.
Initialisation: On a: $u_0=-{1}/{6}$.    De plus: $u_1=f(u_0)=-{1}/{12}$
On a bien $u_0\text"<"u_{1}$. Donc $Q_{0}$ est vraie.
Hérédité:
Soit $n$ un entier naturel, supposons que $Q_n$ soit vraie.
$u_n\text"<"u_{n+1}$.
Or, d'après le 2, $u_n$ et $u_{n+1}$ sont dans $]{-{1}/{3};0}[$.
Donc, comme $f$ est strictement croissante sur $[-{1}/{3};0]$, on a: $f(u_n)\text"<"f(u_{n+1})$.
Soit: $u_{n+1}\text"<"u_{n+2}$.
Donc $Q_{n+1}$ est vraie.
Conclusion: pour tout naturel $n$, $u_n\text"<"u_{n+1}$.

Méthode 2: Démontrons directement que, pour tout naturel $n$ , la propriété $Q_n$ est vraie.
Soit $n$ un entier naturel.
On a:    $u_n\text"<"u_{n+1}$ $⇔$ $0\text"<"u_{n+1}-u_n$ $⇔$ $0\text"<"{u_n}^2+{2}/{3}u_n-u_n$ $⇔$ $0\text"<"{u_n}^2-{1}/{3}u_n$
Or $x^2-{1}/{3}x$ est un trinôme, qui se factorise en $x(x-{1}/{3})$, et qui admet donc comme racines 0 et ${1}/{3}$.
Comme son coefficient dominant 1 est strictement positif, ce trinôme est strictement positif à l'extérieur de ses racines, en particulier pour $x$ dans $]-{1}/{3};0[$.
Or, d'après le 2, $u_n$ est dans $]{-{1}/{3};0}[$.
Donc l'inégalité $0\text"<"{u_n}^2-{1}/{3}u_n$ est vraie, et par là, l'inégalité $u_n\text"<"u_{n+1}$ est vraie également.
Et ceci se vérifie pour tout naturel $n$.

Quelle que soit la méthode utilisée, on peut donc conclure que la suite $(u_n)$ est strictement croissante.

4. Clique ICI pour revoir l'essentiel sur croissance, majoration et convergence.
Nous venons de montrer que la suite $(u_n)$ est strictement croissante.
Or, d'après le 2, elle est majorée par 0.
Donc elle est convergente

5. On pose: $\lim↙{n→+∞}(u_n)=l$.
D'où: $\lim↙{n→+∞}(u_{n+1})=l$, et $\lim↙{n→+∞}(f(u_{n}))=l^2+{2}/{3}l$.
Par passage à la limite dans l'égalité $u_{n+1}=f(u_n)$, on obtient alors: $l=l^2+{2}/{3}l$.
Or: $l=l^2+{2}/{3}l$ $⇔$ $0=l^2-{1}/{3}l$ $⇔$ $0=l(l-{1}/{3})$ $⇔$ $l=0$ ou $l={1}/{3}$.

6. On sait que, pour tout naturel $n$, $0\text">"u_n$.
Par conséquent: $0≥\lim↙{n→+∞}(u_n)$.
Et par là, $l={1}/{3}$ est impossible. La seule valeur possible pour $l$ est 0.

Conclusion: $\lim↙{n→+∞}(u_n)=0$.