Corrigé

1.a. Clique ICI pour revoir l'essentiel sur la démonstration par récurrence.
Supposons que $u_0=-3$. Montrons que, pour tout entier naturel $n$, $u_n=-3$.
Soit $P_n$ la propriété: $u_n=-3$.
Démontrons par récurrence que, pour tout naturel $n$ , la propriété $P_n$ est vraie.
Initialisation: $P_{0}$ est vraie (évident).
Hérédité:
Soit $n$ un entier naturel, supposons que $P_n$ soit vraie.
On a donc: $u_n=-3$.
Comme $u_{n+1}={u_n+6}/{u_n+2}$, on obtient: $u_{n+1}={-3+6}/{-3+2}=-3$.
Donc $P_{n+1}$ est vraie.
Conclusion: pour tout naturel $n$, $u_n=-3$.

Si l'on suppose que $u_0=2$, on montrerait de même que pour tout entier naturel $n$, $u_n=2$.

Par conséquent, si $u_0=-3$ ou $u_0=2$, alors la suite $(u_n)$ est constante.

1.b. On suppose que $u_0≠-3$ et $u_0≠2$.
Montrons que, pour tout entier naturel $n$, $u_n≠-3$ et $u_n≠2$.
Soit $Q_n$ la propriété $u_n≠-3$ et $u_n≠2$.
Démontrons par récurrence que, pour tout naturel $n$ , la propriété $Q_n$ est vraie.
Initialisation: $Q_{0}$ est vraie (évident).
Hérédité:
Soit $n$ un entier naturel, supposons que $Q_n$ soit vraie.
On a donc: $u_n≠-3$ et $u_n≠2$.
Raisonnons par l'absurde pour montrer que $Q_{n+1}$ est vraie.
Nous allons donc supposer que $Q_{n+1}$ est fausse et montrer que c'est absurde.
Or $Q_{n+1}$ est fausse si et seulement si $u_{n+1}=-3$ ou $u_{n+1}=2$.
Supposons par exemple que $u_{n+1}=-3$.
Comme $u_{n+1}={u_n+6}/{u_n+2}$, on obtient: $-3={u_n+6}/{u_n+2}$.
Soit: $-3u_n-6=u_n+6$, et donc: $-3=u_n$, ce qui est contraire à l'hypothèse $Q_n$.
Donc nécessairement, on a: $u_{n+1}≠-3$.
La seule possibilité est alors de supposer que $u_{n+1}=2$. On obtient alors facilement $2=u_n$, ce qui est aussi contraire à l'hypothèse $Q_n$.
Donc finalement, supposer que $Q_{n+1}$ est fausse est absurde.
Et donc $Q_{n+1}$ est vraie.
Conclusion: pour tout naturel $n$, $u_n≠-3$ et $u_n≠2$.

2.a. Soit $n$ un entier naturel.
$v_{n+1}={u_{n+1}+3}/{u_{n+1}-2}={{u_n+6}/{u_n+2}+3}/{{u_n+6}/{u_n+2}-2}={{u_n+6+3u_n+6}/{u_n+6-2u_n-4}={4u_n+12}/{-u_n+2}=(-4){u_{n}+3}/{u_{n}-2}$.
Donc $v_{n+1}=-4v_n$.

2.b. Clique ICI pour revoir l'essentiel sur les suites géométriques.
On a donc $v_{n+1}=-4v_n$ pour tout entier naturel $n$, et par là, la suite $(v_n)$ est géométrique de raison $-4$.
Attention! La raison n'est pas positive! D'où la difficulté de l'exercice...

2.c. D'après le 2.b., on a: $v_n=v_0(-4)^n$, pour tout $n$ entier naturel. D'où: $|v_n|=|v_0|.4^n$.
On sait que: $|v_0|≥0$. Or, $v_0={u_{0}+3}/{u_{0}-2}$; et comme $u_0≠-3$, on a: $v_0≠0$. Et donc: $|v_0|\text">"0$.
Par ailleurs, comme $4\text">"1$, on a: $\lim↙{n→+∞}4^n=+∞$.
Donc finalement, on en déduit que: $\lim↙{n→+∞}|v_n|=+∞$.

2.d. $v_n=1$ $⇔$ ${u_{n}+3}/{u_{n}-2}=1$ $⇔$ $-2=3$, ce qui est absurde.
Donc $v_n≠1$ pour tout naturel $n$.
De l'égalité $v_n={u_{n}+3}/{u_{n}-2}$, on déduit facilement que $u_n={2v_{n}+3}/{v_{n}-1}$.

2.e. Améliorons l'écriture de $u_n$ pour déterminer sa limite.
On a: $u_n={v_n(2+{3}/{v_n})}/{v_n(1-{1}/{v_{n}})}={2+3{1}/{v_n}}/{1-{1}/{v_n}}$.
Or, on a vu que $\lim↙{n→+∞}|v_n|=+∞$.
Par conséquent: $\lim↙{n→+∞}{1}/{|v_n|}=0$. Et donc: $\lim↙{n→+∞}|{1}/{v_n}|=0$, et $\lim↙{n→+∞}-|{1}/{v_n}|=0$.
Or: $-|{1}/{v_n}|≤{1}/{v_n}≤|{1}/{v_n}|$.
Donc, d'après le théorème des gendarmes, on a: $\lim↙{n→+∞}{1}/{v_n}=0$.
Et finalement, on peut conclure que: $\lim↙{n→+∞}(u_n)={2+3×0}/{1-0}=2$.
Soit: $\lim↙{n→+∞}(u_n)=2$.

3 Un algorithme convenable:

$I$ ← $0$
Tant que $I\text"<"N$
   $U$ ← ${U+6}/{U+2}$
   $I$ ← $I+1$
Fin du Tant que

Un programme en PYTHON

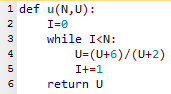
Par exemple, pour $n=7$ et $u_0=25$, u(7,25) retourne 1.9997493324614464