 Suites
Suites
A SAVOIR: le cours sur les suites
Exercice 3
Un exercice de base, assez simple, sur une suite de référence...
Un objet valant $1\,000$ euros décote de 5% par an.
Soit $u_n$ la valeur de l'objet (en euros) au bout de $n$ années. Ainsi, $u_0=1\,000$.
1.a. Exprimer $u_{n+1}$ en fonction de $u_n$ pour tout naturel $n$.
1.b. Qu'en déduire concernant la suite $(u_n)$?
1.c. Exprimer $u_{n}$ en fonction de $n$ .
1.d. Donner le sens de variation de $(u_n)$ ainsi que sa limite.
2.a. Ecrire l'algorithme d'un programme permettant de déterminer la plus petite valeur $n_0$ telle que $u_{n_0}<500$.
2.b. Programmer un tel programme sur votre calculatrice (langage au choix) et donner la valeur de $n_0$ proposée.
Corrigé
Clique ICI pour relire un exemple du cours similaire.
1.a. Pour tout naturel $n$: $u_{n+1}=u_n-{5}/{100}×u_n=(1-{5}/{100})×u_n=0,95×u_n$.
Soit: $u_{n+1}=0,95×u_n$
1.b. Par conséquent, la suite $(u_n)$ est géométrique de raison $r=0,95$ de premier terme $u_0=1\,000$.
1.c. Et par là, pour tout naturel $n$: $u_n=1\,000× 0,95^n$.
1.d. Comme $0$<$0,95$<$1$, alors $(0,95^n)$ est strictement décroissante.
Et comme $1\,000$>$0$, $(u_n)$ est également strictement décroissante.
Par ailleurs:
Comme $0≤0,95$<$1$, on a: $\lim↙{n→+∞}(r^n)=0$.
Et par là: $\lim↙{n→+∞}(u_n)$$=1\,000×0$ $=0$.
2.a. Nous proposons deux algorithmes possibles.
A la fin de chacun d'eux, la variable N contient la valeur $n_0$ cherchée.
Le premier utilise
la formule de récurrence.
N ← 0
U ← $1\,000$
Tant que U$≥500$
U ← U$× 0,95$
N ← N+1
Fin du Tant que
Le second utilise
la formule explicite.
N ← 0
Tant que $1\,000× 0,95^N≥500$
N ← N+1
Fin du Tant que
2.b.
Exemples de programmes utilisant la formule explicite.
La dernière ligne de ces programmes (qui n'apparaît pas dans les algorithmes précédents) permet d'afficher la valeur finale de N.
programmes en BASIC
Pour une Casio:
$0→N$
While $1\,000× 0,95^N≥500$
$N+1→N$
WhileEnd
N
Pour une TI:
$0→N$
While $1\,000× 0,95^N≥500$
$N+1→N$
End
Disp N
programme en PYTHON
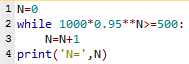
Les trois programmes donnent une valeur de N égale à 14.