Représentations paramétriques et équations cartésiennes
Représentations paramétriques et équations cartésiennes
A SAVOIR: le cours sur Représentations paramétriques et équations cartésiennes
Exercice 4
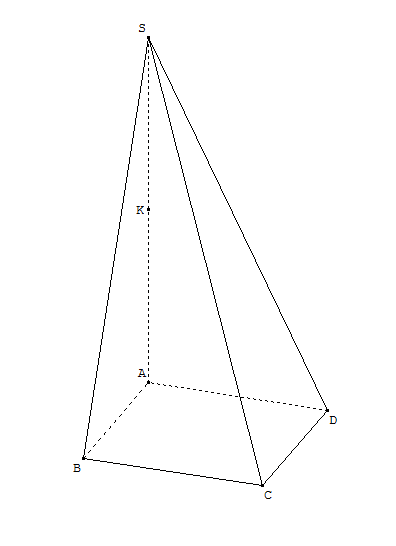
L'espace est muni du repère orthonormal (A, B, D, K).
ABCDS est une pyramide à base carrée ABCD, telle que S a pour coordonnées (0 ; 0 ; 2) et C a pour coordonnées (1 ; 1 ; 0).
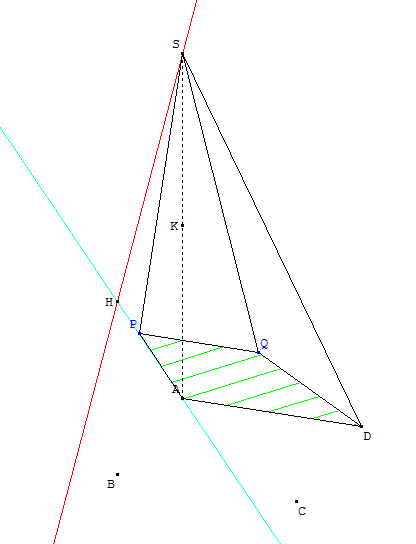
- Soit P le point de la droite (SB) de cote ${2}/{3}$. Construire le point P sur la figure.
-
Soit Q le point d’intersection du plan (APD) et de la droite (SC).
Expliquer pourquoi (APD) et (BPC) se coupent selon la droite (PQ).
On admettra que les droites (AD) et (PQ) sont parallèles.
Construire le point Q sur la figure. - On admet que C a pour coordonnées (1 ; 1 ; 0) et que P a pour coordonnées (${2}/{3}$ ; 0 ; ${2}/{3}$).
Déterminer une représentation paramétrique de la droite (SC).
Déterminer une représentation paramétrique de la droite (PQ).
Montrer que Q a pour coordonnées (${2}/{3}$ ; ${2}/{3}$ ; ${2}/{3}$). - Sans calcul, expliquer pourquoi le trapèze APQD a pour hauteur AP.
Montrer que l'aire $s$ du trapèze APQD vaut ${5}/{9}√{2}$. - Déterminer une équation cartésienne du plan (APD), ainsi qu'une représentation paramétrique de la droite $d$ orthogonale à ce plan et passant par S.
- Déterminer les coordonnées du point H, pied de la hauteur (SH) de la pyramide PQDAS issue de S.
- Déterminer le volume de la pyramide PQDAS.
Corrigé
L'espace est muni d'un repère orthonormal, ce qui autorise tous calculs de distances, normes ou produits scalaires.
- Clique ICI pour revoir quelques notions sur les coordonnées dans l'espace.
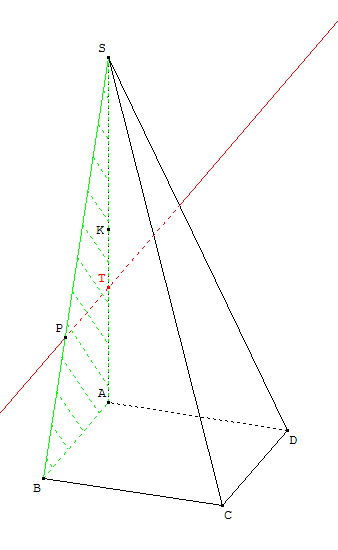
P est sur droite (SB). Or la droite (SB) est dans le plan (ABS). Donc le point P a pour ordonnée 0. Comme sa cote est ${2}/{3}$, il suffit de partir de A, de monter de ${2}/{3}$ selon l'axe (AS). On arrive alors à un point T sur la figure. On trace alors une parallèle à la droite (AB). Elle coupe (BS) en P.
-
Clique ICI pour revoir le cours sur l'intersection de 2 plans.
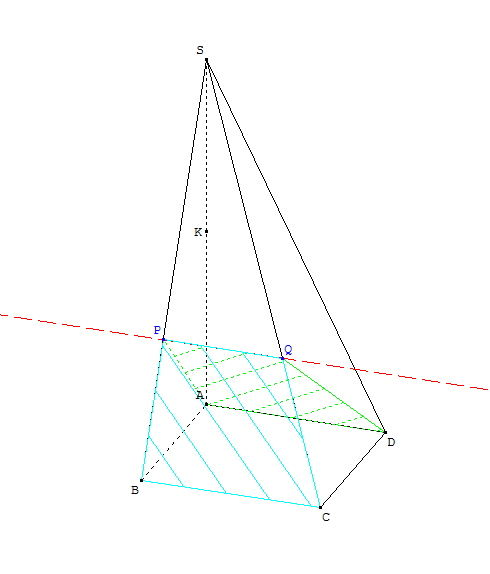
Q est le point d’intersection du plan (APD) et de la droite (SC).
Q appartient donc au plan (APD).
Et il appartient aussi à la droite (SC). Et comme (SC) est clairement dans le plan (BPC), le point Q appartient donc au plan (BPC).
Q appartient donc à la fois au plan (APD) et au plan (BPC).
Or, P appartient aussi à ces 2 plans (c'est évident).
Donc (APD) et (BPC) se coupent selon la droite (PQ).
On a admis que cette droite (PQ) est parallèle à (AD).
Cela permet de construire le point Q.
- Clique ICI pour revoir quelques notions sur les représentations paramétriques (de droites et de plans).
On obtient facilement: ${SC}↖{→}$(1 ; 1 ; -2).
Or C a pour coordonnées (1 ; 1 ; 0).
Donc la droite (SC) admet pour représentation paramétrique $\{\table x=1+t; y=1+t; z=-2t$
Par ailleurs, P a pour coordonnées (${2}/{3}$ ; 0 ; ${2}/{3}$).
Or (AD) et (PQ) sont parallèles, et on a facilement: ${AD}↖{→}$(0 ; 1 ; 0).
Donc la droite (PQ) admet pour représentation paramétrique $\{\table x={2}/{3}; y=t'; z={2}/{3}$
Les coordonnées de Q qui appartient aux 2 droites vérifient les 2 représentations paramétriques:
Donc: $\{\table {2}/{3}=1+t; t'=1+t; {2}/{3}=-2t$
Et par là: $\{\table -{1}/{3}=t; t'={2}/{3}; -{1}/{3}=t$
En reportant $t=-{1}/{3}$ dans la représentation paramétrique de (SC), on obtient: Q(${2}/{3}$ ; ${2}/{3}$ ; ${2}/{3}$). - Comme les droites (AD) et (PQ) sont parallèles, les bases du trapèze APQD sont AD et PQ.
Montrons que sa hauteur est AP.
La droite (AP) appartient clairement au plan (ABK).
Or, comme (A, ${AB}↖{→}$, ${AD}↖{→}$, ${AK}↖{→}$) est un repère orthonormal, le plan (ABK) est orthogonal à la droite (AD).
Donc la droite (AP) est orthogonal à la droite (AD).
Et par là, AP est bien la hauteur du trapèze APQD.
Reste à calculer toutes ces distances pour obtenir l'aire cherchée.
On obtient facilement : ${AD}↖{→}$(0 ; 1 ; 0), ${PQ}↖{→}$(0 ; ${2}/{3}$ ; 0), ${AP}↖{→}$(${2}/{3}$ ; 0 ;${2}/{3}$)
D'où: $AD=√{0^2+1^2+0^2}=1$, et de même: $PQ={2}/{3}$, et $AP={2}/{3}√{2}$.
D'où l'aire cherchée: $s ={AD+PQ}/{2}×AP={1+{2}/{3}}/{2}×{2}/{3}√{2}={{5}/{3}}/{2}×{2}/{3}√{2}={5}/{9}√{2}$ - (APD) passe par A(0,0,0) et a pour vecteurs directeurs ${AD}↖{→}$(0 ; 1 ; 0) et ${AP}↖{→}$(${2}/{3}$ ; 0 ;${2}/{3}$).
Donc (APD) admet pour représentation paramétrique $\{\table x={2}/{3}t'; y=t; z={2}/{3}t'$
Or $\{\table x={2}/{3}t'; y=t; z={2}/{3}t'$ $⇔$ $\{\table x={2}/{3}t'; y=t; {3}/{2}z=t'$ $⇔$ $\{\table x={2}/{3}×{3}/{2}z; y=t; {3}/{2}z=t'$
La première ligne équivaut à: $x-z=0$, qui est une équation cartésienne de (APD).
Le plan (APD), d'équation cartésienne $x-z=0$, a donc pour vecteur normal ${n}↖{→}$(1 ; 0 ; -1).
Et, comme $d$ est orthogonale à (APD), ce vecteur est un vecteur directeur de $d$.
Or $d$ passe par S(0 ; 0 ; 2).
Donc la droite $d$ admet pour représentation paramétrique $\{\table x=t; y=0; z=2-t$
- Le point H est le pied de la hauteur (SH) de la pyramide PQDAS issue de S.
Donc H appartient au plan (APD) et à la droite orthogonale à ce plan qui passe par S, c'est à dire $d$.
Donc, si H a pour coordonnées ($x,y,z$), on a: $x-z=0$, et de plus, il existe un réel $t$ tel que $\{\table x=t; y=0; z=2-t$
D'où: $t-(2-t)=0$, et par là: $t=1$.
Par conséquent: $\{\table x=1; y=0; z=1$.
Donc H(1 ; 0 ; 1).
Remarque: l'angle droit en H est déformé à cause de la perspective cavalière!
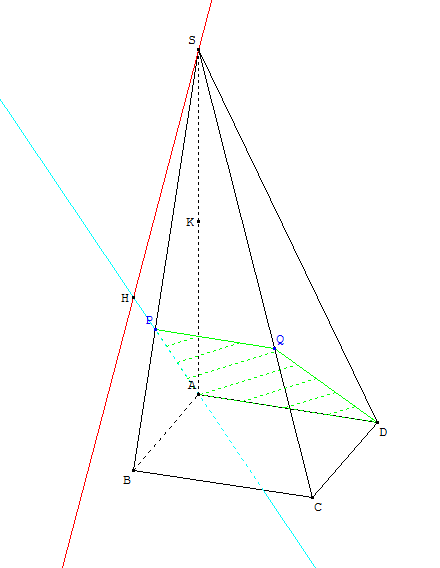
- Il est clair que la pyramide PQDAS a pour base APQD et pour hauteur HS.
Son volume est donc: $v={1}/{3}×s×HS$
Soit: $v={1}/{3}×{5}/{9}√{2}×√{(0-1)^2+(0-0)^2+(2-1)^2}={5}/{27}√{2}×√{2}$
Soit: $v={10}/{27}$