Représentations paramétriques et équations cartésiennes
Représentations paramétriques et équations cartésiennes
A SAVOIR: le cours sur Représentations paramétriques et équations cartésiennes
Exercice 7
Un architecte veut réaliser un toit incliné triangulaire selon le modèle ci-dessous.
Un mat situé derrière le toit retient ce dernier par l'intermédiaire d'un cable d'acier tendu entre le sommet de ce mat et le sol.
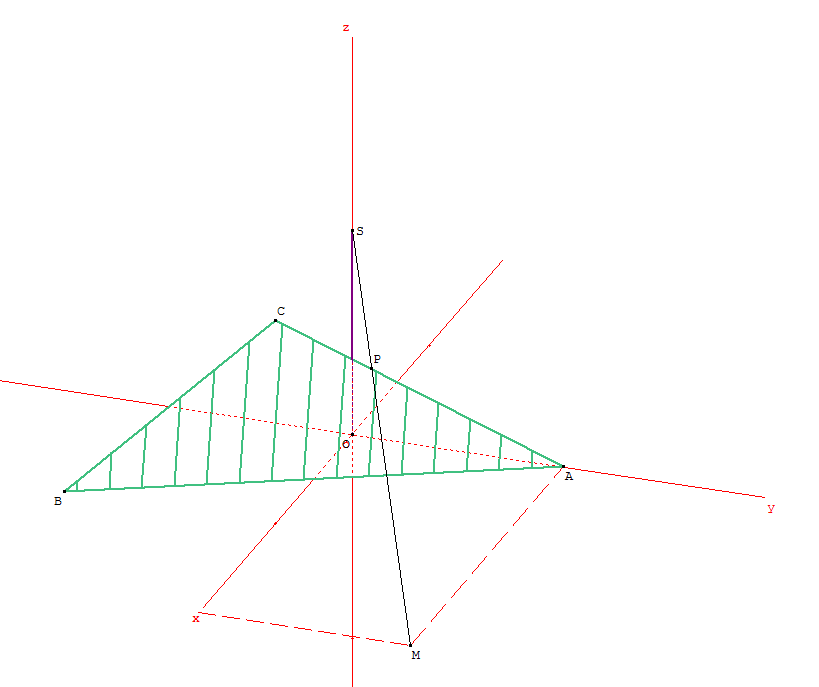
L'architecte simplifie le dessin selon la figure suivante. Le toit est le triangle ABC.
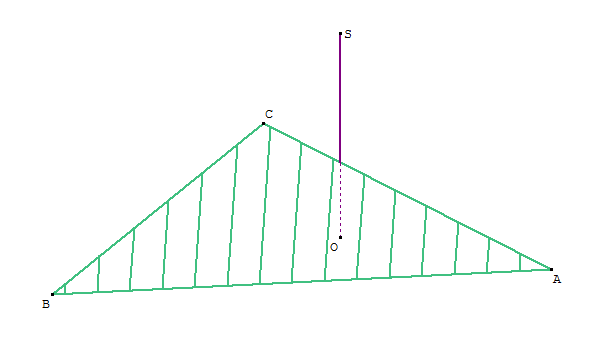
Le segment [AB] est au sol. Le point C est le sommet du toit.
Un filin métallique (non représenté pour l'instant) sera tendu entre le sommet S du mât [OS] et le sol (OAB).
Le filin sera orthogonal au toit.
Ce filin sera fixé au sol au point M, et au toit au point P.
Le but de l'exercice est de déterminer les positions exactes des points M et P.
L'espace est muni du repère orthonormal (O, I, J, K).
A a pour coordonnées (0 ; 1 ; 0), B a pour coordonnées (1 ; $-1$ ; 0),
C a pour coordonnées (1 ; $0$ ; 1), S a pour coordonnées (0 ; 0 ; 1),
- Les points A, B et C sont-ils alignés?
- Le vecteur ${n}↖{→}$ ($-2$ ; $-1$ ; 1) est-il un vecteur normal au plan (ABC)?
- Déterminer une équation paramétrique de la droite $d$ passant par S et perpendiculaire au plan (ABC).
- Soit M le point d'intersection de la droite $d$ et du plan (OAB).
Déterminer les coordonnées du point M. - Déterminer une équation cartésienne du plan (ABC).
-
Soit P le point d'intersection de la droite $d$ et du plan (ABC).
Montrer que P est sur la droite (CA). - Calculer la distance CP.
- Compléter le dessin proposé en plaçant précisément les points M et P.
Corrigé
- On obtient facilement : ${AB}↖{→}$( 1 ; $-2$ ; 0 ) ${AC}↖{→}$( 1 ; $-1$ ; 1 ).
${AB}↖{→}$ et ${AC}↖{→}$, vecteurs non nuls dont les coordonnées ne sont pas proportionnellles, ne sont donc pas colinéaires.
Les points A, B et C ne sont donc pas alignés.
C'est pourquoi nous pouvons parler du plan (ABC) dans les questions qui suivent...
Notons de plus que les vecteurs ${AB}↖{→}$ et ${AC}↖{→}$ forment donc un couple de vecteurs directeurs du plan (ABC).
- Clique ICI pour revoir le cours sur les vecteurs normaux à un plan.
On a: ${AB}↖{→}.{n}↖{→}=1×(-2)-2×(-1)+0×1=0$ ${AC}↖{→}.{n}↖{→}=1×(-2)-1×(-1)+1×1=0$
Or ${AB}↖{→}$ et ${AC}↖{→}$ forment un couple de vecteurs directeurs du plan (ABC).
Donc le vecteur ${n}↖{→}$ ($-2$ ; $-1$ ; 1) est effectivement un vecteur normal au plan (ABC). - Clique ICI pour revoir quelques notions sur les représentations paramétriques (de droites et de plans).
La droite $d$ passe par S (0 ; 0 ; 1).
Or elle est perpendiculaire au plan (ABC) de vecteur normal ${n}↖{→}$ ($-2$ ; $-1$ ; 1).
Donc $d$ admet pour représentation paramétrique $\{\table x=-2t; y=-t;z=t+1$
- Le point M ( $x;y;z$) appartient à la fois à la droite $d$ et au plan (OAB).
Il existe donc un réel $t$ tel que $\{\table x=-2t; y=-t;z=t+1$.
Et comme le plan (OAB) a pour équation cartésienne: $z=0$ (évident),
on obtient: $\{\table x=-2t; y=-t;0=t+1$.
Et par là: $\{\table x=2; y=1;t=-1$.
Donc M (2 ; 1 ; 0).
- Déterminons une équation cartésienne du plan (ABC).
${n}↖{→}$ ($-2$ ; $-1$ ; 1) est un vecteur normal de (ABC).
Le plan (ABC) admet donc pour une équation cartésienne du type: $-2×x-1×y+z+d=0$.
Or A (0 ; 1 ; 0) est dans P; donc: $-2×0-1×1+0+d=0$, d'où: $d=1$.
Donc (ABC) admet pour équation cartésienne $-2×x-1×y+z+1=0$. -
Déterminons les coordonnées de P ( $x;y;z$).
P est le point d'intersection de la droite $d$ et du plan (ABC).
Il existe donc un réel $t$ tel que $\{\table x=-2t; y=-t;z=t+1$.
Or le plan (ABC) a pour équation cartésienne: $-2×x-1×y+z+1=0$.
Donc on obtient: $-2×(-2t)-1×(-t)+t+1+1=0$.
Et donc: $t={-1}/{3}$.
Et par conséquent: $\{\table x={2}/{3}; y={1}/{3};0={2}/{3}$.
Donc P(${2}/{3}$ ; ${1}/{3}$ ; ${2}/{3}$).
Montrons que P est sur la droite (CA).
On obtient facilement : ${CP}↖{→}$( $-{1}/{3}$ ; ${1}/{3}$ ; $-{1}/{3}$ ) ${AC}↖{→}$( 1 ; $-1$ ; 1 ).
On constate alors que: ${CP}↖{→}=-{1}/{3}{AC}↖{→}$.
${CP}↖{→}$ et ${AC}↖{→}$ sont donc colinéaires.
Donc les points A, P et C sont alignés.
Et par là, P est sur la droite (CA). - On calcule finalement : ${CP}↖{→}.{CP}↖{→}=(-{1}/{3})^2+(-{1}/{3})^2+(-{1}/{3})^2={1}/{3}$ et par là: $CP=√{{1}/{3}}$
- Pour compléter la figure, on trace d'abord les axes du repère.
L'axe Oy passe par O et A (évident).
L'axe Oz passe par O et S (évident).
Pour déterminer l'axe Ox, on place d'abord le point T (0 ; $-1$ ; 0).
Puis on trace la droite (TB).
L'axe Ox passe par O et est parallèle à la droite (TB)).
Une illusion d'optique laisse croire, à tort, que ces droites ne sont pas parallèles sur le dessin.
La figure est alors la suivante.
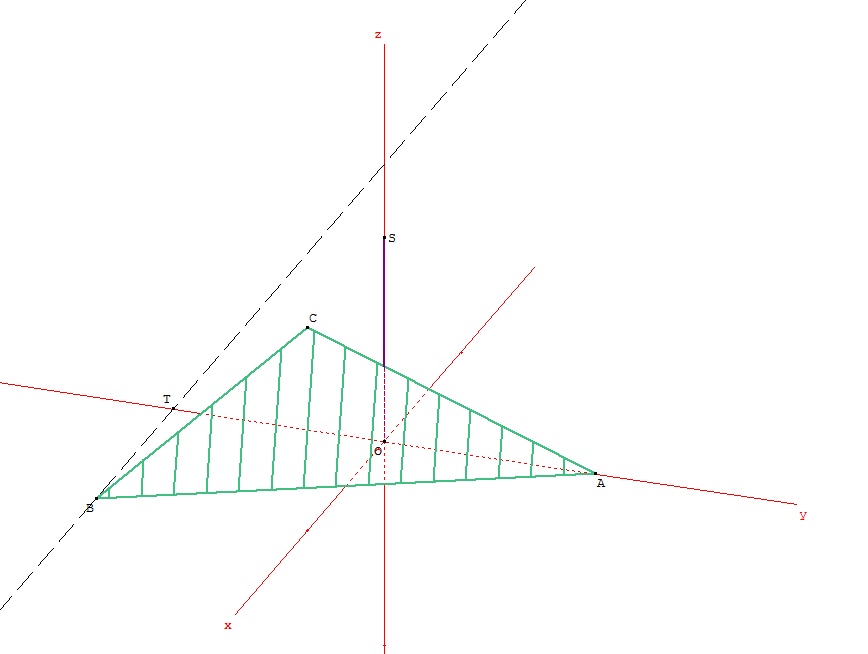
La figure terminée est finalement la suivante (on a placé M, puis P).