Représentations paramétriques et équations cartésiennes
Représentations paramétriques et équations cartésiennes
A SAVOIR: le cours sur Représentations paramétriques et équations cartésiennes
Exercice 5
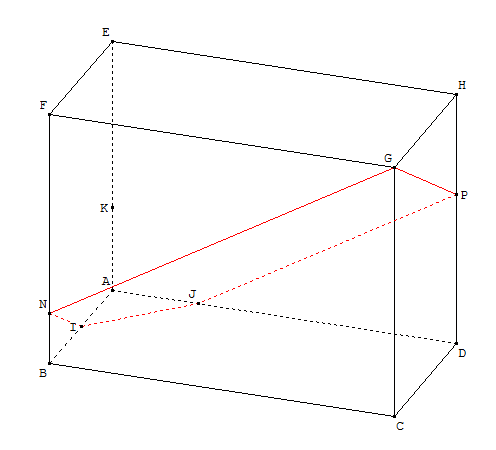
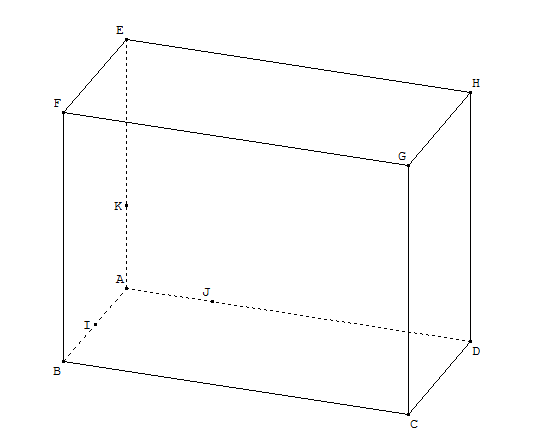
L'espace est muni du repère orthonormal (A, I, J, K).
ABCDEFGH est un parallélépipède rectangle, tel que
B a pour coordonnées (2 ; 0 ; 0), C a pour coordonnées (2 ; 4 ; 0), E a pour coordonnées (0 ; 0 ; 3) et F a pour coordonnées (2 ; 0 ; 3).
- On considère le point N, intersection du plan (IJG) et de la droite (BF).
- Cette question ne nécessite aucun calcul
- Donner, sans justifier, un plan auquel appartiennent les droites (IJ) et (BC).
- On admettra que les droites (IJ) et (BC), coplanaires, sont sécantes en un point M.
Déterminer, en justifiant, la droite qui constitue l'intersection du plan (IJG) et du plan (BCG). -
Construire, sans justifier, le point N.
- Nous allons vérifier que la construction de N est correcte en déterminant les coordonnées de N.
-
Il est clair que G a pour coordonnées (2 ; 4 ; 3).
Par ailleurs, le plan (IJG) admet pour vecteurs directeurs ${IJ}↖{→}$ et ${IG}↖{→}$.
Montrer que le vecteur ${n}↖{→}$(1 ; 1 ;$-{5}/{3}$) est normal au plan (IJG). - Déterminer une équation du plan (IJG).
- Déterminer les coordonnées du point N, intersection du plan (IJG) et de la droite (BF).
-
Il est clair que G a pour coordonnées (2 ; 4 ; 3).
- On admettra qu'un plan coupe 2 plans parallèles selon 2 droites parallèles.
Tracer, sans justifier, la section du pavé ABCDEFGH par le plan (IJG).
Corrigé
- Les droites (IJ) et (BC) appartiennent au plan (AIJ), qui contient la face inférieure du pavé.
- Clique ICI pour revoir le cours sur l'intersection de 2 plans.
Les droites (IJ) et (BC) sont sécantes en un point M.
Donc, comme (IJ) est dans le plan (IJG), le point M est aussi dans le plan (IJG).
Et de même, comme (BC) est dans le plan (BCG), le point M est aussi dans le plan (BCG).
Par ailleurs, le point G est évidemment dans les plans (IJG) et (BCG).
Nous avons donc trouvé 2 points, M et G, qui appartiennent à la fois à (IJG) et à (BCG).
Donc les plans (IJG) et (BCG) se coupent selon la droite (MG).
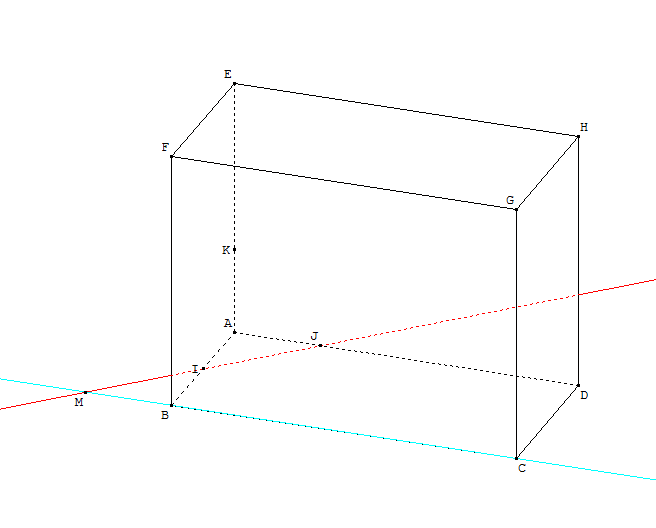
- La construction est ci-dessous.
Explication non demandée: Le point N est sur (BF), et donc dans le plan (BCG). Or il est aussi dans (IJG). Donc il est dans l'intersection de (IJG) et (BCG), c'est à dire sur (MG). Finalement, il est à l'intersection des droites (MG) et (BF).
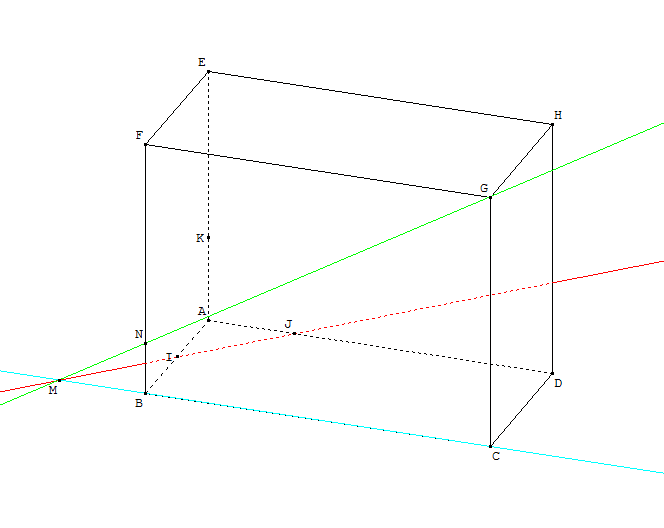
Remarque: nous pouvons calculer rapidement la distance BN en utilisant 2 fois le théorème de Thalès.
$\{\table (AJ)\/\/(BM); I∈[AB]; I∈[JM]$ donc: ${MB}/{JA}={BI}/{AI}$ soit: ${MB}/{1}={1}/{1}$ et donc: MB=1
$\{\table (BN)\/\/(CG); B∈[MC]; N∈[MG]$ donc: ${NB}/{GC}={BM}/{CM}$ soit: ${NB}/{3}={1}/{5}$ et donc: $NB={3}/{5}$
Nous retrouverons péniblement cette valeur dans la question 2.
-
L'espace est muni d'un repère orthonormal, ce qui autorise tous calculs de distances, normes ou produits scalaires.
- Clique ICI pour revoir le cours sur les vecteurs normaux à un plan.
On obtient facilement: ${IJ}↖{→}$($-1$ ; 1 ; 0).
On calcule alors: ${IJ}↖{→}.{n}↖{→}=(-1)×1+1×1+0×=0$.
De même, on obtient facilement: ${IG}↖{→}$(1 ; 4 ; 3).
On calcule alors: ${IG}↖{→}.{n}↖{→}=1×1+4×1+3×(-{5}/{3}=0$.
Or le plan (IJG) admet pour vecteurs directeurs ${IJ}↖{→}$ et ${IG}↖{→}$.
Donc le vecteur ${n}↖{→}$ est normal au plan (IJG). - Clique ICI pour revoir quelques notions sur les équations cartésiennes de plan.
Comme ${n}↖{→}$(1 ; 1 ;$-{5}/{3}$) est normal à (IJG), ce dernier admet une équation du type: $x+y-{5}/{3}z+d=0$.
Or, commme I (1 ; 0 ; 0) est dans (IJG), ses coordonnées vérifient cette équation.
Donc: $1+0-{5}/{3}×0+d=0$, et par là: $d=-1$.
Donc (IJG) a pour équation cartésienne: $x+y-{5}/{3}z-1=0$. - Clique ICI pour revoir quelques notions sur les représentations paramétriques (de droites et de plans).
On obtient facilement: ${BF}↖{→}$(0 ; 0 ; 3).
Or B a pour coordonnées (2 ; 0 ; 0).
Donc la droite (BF) admet pour représentation paramétrique $\{\table x=2; y=0; z=3t$
Le point N, intersection du plan (IJG) et de la droite (BF), voit ses coordonnées ($x$ ; $y$ ; $z$) satisfaire à l'équation cartésienne du plan et à la représentation paramétrique:
Donc: $\{\table x=2; y=0; z=3t$ et $x+y-{5}/{3}z-1=0$.
D'où: $2+0-{5}/{3}×3t-1=0$.
Et par là: $t={1}/{5}$.
On obtient donc finalement: $\{\table x=2; y=0; z={3}/{5}$.
Donc N a pour coordonnées (2 ; 0 ; ${3}/{5}$).
Nous retrouvons la valeur remarquée dans la question 1.
- Clique ICI pour revoir le cours sur les vecteurs normaux à un plan.
- La section est INGPJ, en rouge sur le dessin.
Vous noterez que (PJ) et (GN) sont parallèles, car le plan (IJG) coupe 2 faces parallèles selon 2 droites parallèles.
Pour une raison analogue, (IN) est parallèle à (PG)