 Equations et inéquations
Equations et inéquations
Cette leçon a été traitée en grande partie en classe de seconde.Les exercices la concernant sont disséminés dans les autres chapitres.
Définition
Le domaine de définition d'une fonction $f$, souvent noté $\D_f$, est l'ensemble de tous les réels $x$ pour lesquels $f(x)$ existe.
Exemple
Quel est le domaine de définition de chacune des fonctions suivantes?
$f(x)=x^2+2x+3$ $g(x)={1}/{x-3}$ $h(x)=√{x-5}$
Corrigé
- $f(x)$ existe pour tout réel $x$. Donc $\D_f$=ℝ.
-
$g(x)$ est un quotient. Son dénominateur ne doit pas être nul.
Or: $x-3=0$ $⇔$ $x=3$.
Donc: $\D_g=]-∞;3[∪]3;+∞[=ℝ\\\{3\}$. -
$h$ est une racine carrée. ce qui est sous le radical doit être positif ou nul.
Or: $x-5≥0$ $⇔$ $x≥5$.
Donc: $\D_h=[5;+∞[$.
Définition
Le domaine d'étude d'une équation écrite sous la forme $g(x)=d(x)$ est l'intersection des domaines de définition des fonctions $g$ et $d$.
Le domaine d'étude, souvent noté $\D_E$ , est l'ensemble dans lequel on recherche les solutions de l'équation.
Exemple
Quel est le domaine d'étude de chacune des équations suivantes?
$x^2+2x+3=10$ ${1}/{x-3}=2x$ $√{x-5}=√{x-8}$
Corrigé
- Equation $x^2+2x+3=10$
Comme $x^2+2x+3$ et $10$ existent pour tout réel $x$, on obtient: $\D_E$=ℝ. -
Equation ${1}/{x-3}=2x$
${1}/{x-3}$ n'existe que pour $x≠3$. De plus, $2x$ existe pour tout $x$.
On obtient donc: $\D_E=ℝ\\\{3\}$. -
$√{x-5}$ n'existe que pour $x≥5$. De plus, $√{x-8}$ n'existe que pour $x≥8$.
On obtient donc: $\D_E=[8;+∞[$.
A retenir
Lorsqu'il est évident que le domaine d'étude d'une équation est $ℝ$, il est courant de ne pas le citer.
Quand ce n'est pas le cas, le domaine doit être explicité pour bien repérer les valeurs 'interdites'.
Propriété
Voici certaines équations de référence du programme de seconde.
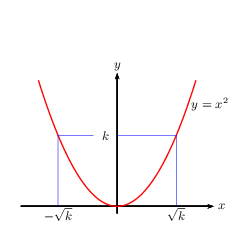
Soit $k$ un réel positif. $x^2=k$ $ ⇔$ $x=-√{k}$ ou $x=√{k}$
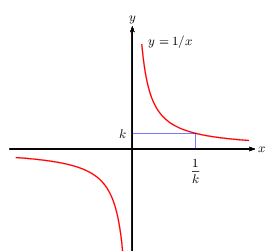
Soit $k$ un réel non nul. ${1}/{x}=k$ $ ⇔$ $x={1}/{k}$
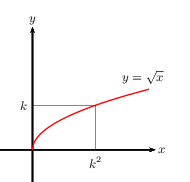
Soit $k$ un réel positif. $√{x}=k$ $ ⇔$ $x=k^2$
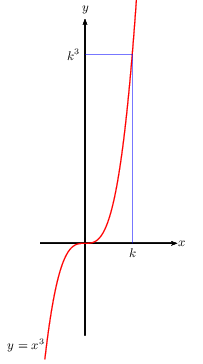
Soit $k$ un réel. $x^3=k^3$ $ ⇔$ $x=k$
Les équations précédentes se résolvent très facilement lorsque l'on connait les courbes représentatives des fonctions carré, inverse, racine carrée et cube.
Par exemple, revoir les débuts des
exercice 1,
exercice 8,
exercice 10
et exercice 12
sur les fonctions de référence de seconde.
Définition
Les équations de référence (au programme) sont les suivantes.
$f(x)=0$ où $f$ est une fonction affine
$f(x)=0$ où $f$ est un polynôme du second degré
$(f(x))^2=k$ où $f$ est une fonction (simple) et $k$ un réel.
${1}/{f(x)}=k$ où $f$ est une fonction (simple) et $k$ un réel.
$√{f(x)}=k$ où $f$ est une fonction (simple) et $k$ un réel.
$(f(x))^3=k^3$ où $f$ est une fonction (simple) et $k$ un réel.
Exemple
Résoudre chacune des équations suivantes.
($E_1$) $-7x-3=0$
($E_2$) $x^2+2x-7=0$ (cours sur les trinômes du second degré à connaitre)
($E_3$) $(x-3)^2=10$ (si besoin, revoir par exemple cet
exercice de seconde)
($E_4$) ${1}/{x-3}=2$ (si besoin, revoir par exemple cet
exercice de seconde)
($E_5$) $√{x-5}=9$ (si besoin, revoir par exemple cet
exercice de seconde)
($E_6$) $(x-1)^3=8$ (si besoin, revoir par exemple cet
exercice de seconde)
Corrigé
- ($E_1$) $-7x-3=0$
Le membre de gauche est une fonction affine. Il est facile d'isoler l'inconnue $x$.
($E_1$) $ ⇔$ $-7x=3$ $⇔$ $x={3}/{-7}$
Donc $\S_1=\{-{3}/{7}\}$. - ($E_2$) $x^2+2x-7=0$
Le membre de gauche de ($E_2$) est un trinôme avec $a=1$, $b=2$ et $c=-7$.
$Δ=b^2-4ac=2^2-4×1×(-7)=32$.
$Δ>0$. Le trinôme a 2 racines
$x_1={-b-√Δ}/{2a}={-2-√{32}}/{2×1}=-1-2√{2}≈-3,8$
et $x_2={-b+√Δ}/{2a}={-2+√{32}}/{2×1}=-1+2√{2}≈1,8$.
Donc $\S_2=\{-1-2√{2};-1+2√{2} \}$
- ($E_3$) $(x-3)^2=10$
L'équation est du type $(f(x))^2=k$. Il est facile de déterminer $f(x)$, puis $x$.
($E_3$) $ ⇔$ $(x-3)^2=10$ $⇔$ $x-3=-√{10}$ ou $x-3=√{10}$
Soit: ($E_3$) $⇔$ $x=3-√{10}$ ou $x=3+√{10}$
Donc $\S_3=\{3-√{10} ; 3+√{10}\}$.
Développer $(x-3)^2$, puis transposer le 10 aurait conduit à la recherche des racines d'un trinôme. La méthode aurait été correcte, mais plus longue!
- ($E_4$) ${1}/{x-3}=2$
L'équation est du type ${1}/{f(x)}=k$. On repère le domaine d'étude ($f(x)$ ne doit pas être nul). Il est ensuite facile de déterminer $f(x)$, puis $x$.
Le domaine d'étude est $\D_4=ℝ\\\{3\}$
Cela implique que 3 ne peut pas être une solution de cette équation.
($E_4$) $ ⇔$ ${1}/{x-3}=2$ $⇔$ $x-3={1}/{2}$
Soit: ($E_4$) $⇔$ $x=3+0,5=3,5$
Donc $\S_4=\{3,5\}$. - ($E_5$) $√{x-5}=9$
L'équation est du type $√{f(x)}=k$. On repère le domaine d'étude ($f(x)$ doit être positif). Il est ensuite facile de déterminer $f(x)$, puis $x$.
Le domaine d'étude est $\D_5=[5;+∞[$
Cela implique que les réels strictement inférieurs à 5 ne peuvent pas être solution de cette équation.
($E_5$) $ ⇔$ $√{x-5}=9$ $⇔$ $x-5=9^2$
Soit: ($E_5$) $⇔$ $x=5+81=86$
Donc $\S_5=\{86\}$. - ($E_6$) $(x-1)^3=8$
L'équation est du type $(f(x))^3=k$. Il est facile de déterminer $f(x)$, puis $x$.
($E_6$) $ ⇔$ $(x-1)^3=8$ $⇔$ $(x-1)^3=2^3$ $⇔$ $x-1=2$
Soit: ($E_6$) $⇔$ $x=1+2=3$
Donc $\S_6=\{3\}$.
A retenir
La résolution d'une équation se ramène généralement à la résolution d'une ou plusieurs équations de référence.
Savoir faire
Pour résoudre une équation, il suffit de transposer certains termes et de se ramener à la résolution d'une équation de référence.
Si la méthode ne fonctionne pas, il est conseillé de transposer le membre de droite pour obtenir une équation du type $f(x)=0$.
En général, il faut alors: soit factoriser $f(x)$, soit l'écrire sous forme d'un quotient. Cela permet souvent de conclure car on se ramène à la résolution d'équations de référence.
Exemple
Résoudre chacune des équations suivantes.
($E_1$) $3(x-1)^2=5$
($E_2$) $x^3=x^2$
($E_3$) $x^2={1}/{x}$
Corrigé
Soit: ($E_1$) $ ⇔$ $x=1-√{{5}/{3}}={3-√{15}}/{3}$ ou $x=1+√{{5}/{3}}={3+√{15}}/{3}$
$\S_1=\{{3-√{15}}/{3};{3+√{15}}/{3}\}$.
A retenir: un produit de facteurs est nul si et seulement l'un des facteurs est nul.
Soit: ($E_2$) $ ⇔$ $x^2=0$ ou $x-1=0$
Soit: ($E_2$) $ ⇔$ $x=0$ ou $x=1$
$\S_2=\{{0;1\}$.
On retrouve le fait que la signoïde représentant la fonction cube et la parabole représentant la fonction carré se coupent aux points d'abscisses 0 et 1.
Donc le domaine d'étude est $\D_3=ℝ\\\{0\}$.
($E_3$) $ ⇔$ $x^2-{1}/{x}=0$ $ ⇔$ ${x^3}/{x}-{1}/{x}=0$
Soit: ($E_3$) $ ⇔$ ${x^3-1}/{x}=0$
A retenir: un quotient est nul si et seulement son numérateur est nul.
Soit: ($E_3$) $ ⇔$ $x^3-1=0$
Soit: ($E_3$) $ ⇔$ $x^3=1$
Soit: ($E_3$) $ ⇔$ $x^3=1^3$ $ ⇔$ $x=1$
$\S_3=\{1\}$.
On retrouve le fait que la parabole représentant la fonction carré et l'hyperbole représentant la fonction inverse se coupent au point d'abscisse 1.
Les définitions et propriétés vues pour les équations se transposent en général aux inéquations.
Définition
Le domaine d'étude d'une inéquation écrite sous la forme $g(x)≤d(x)$ ou $g(x)$<$d(x)$ ou $g(x)≥d(x)$ ou $g(x)$>$d(x)$ est l'intersection des domaines de définition des fonctions $g$ et $d$.
Le domaine d'étude, souvent noté $\D_E$ , est l'ensemble dans lequel on recherche les solutions de l'inéquation.
A retenir
Lorsqu'il est évident que le domaine d'étude d'une inéquation est $ℝ$, il est courant de ne pas le citer.
Quand ce n'est pas le cas, le domaine doit être explicité pour bien repérer les valeurs 'interdites'.
Propriété
Les inéquations de référence du programme de seconde se résolvent très facilement lorsque l'on connait les courbes représentatives des fonctions carré, inverse, racine carrée et cube.
Par exemple, revoir la fin des
exercice 1,
exercice 8,
exercice 10
et exercice 12
sur les fonctions de référence de seconde.
Définition
Les inéquations de référence (au programme) sont les suivantes.
$f(x)≤0$ où $f$ est une fonction affine
$f(x)≤0$ où $f$ est un polynôme du second degré
$(f(x))^2≤k$ où $f$ est une fonction (simple) et $k$ un réel.
${1}/{f(x)}≤k$ où $f$ est une fonction (simple) et $k$ un réel.
$√{f(x)}≤k$ où $f$ est une fonction (simple) et $k$ un réel.
$(f(x))^3≤k^3$ où $f$ est une fonction (simple) et $k$ un réel.
Et en remplaçant $≤$ par < ou $≥$ ou >, on obtient les autres inéquations au programme.
Exemple
Résoudre chacune des inéquations suivantes.
($E_1$) $-7x-3≤0$
($E_2$) $x^2+2x-7≤0$ (cours sur les trinômes du second degré à connaitre)
($E_3$) $(x-3)^2≤10$ (si besoin, revoir par exemple cet
exercice de seconde)
($E_4$) ${1}/{x-3}≤2$ (si besoin, revoir par exemple cet
exercice de seconde)
($E_5$) $√{x-5}≤9$ (si besoin, revoir par exemple cet
exercice de seconde)
($E_6$) $(x-1)^3≤8$
Corrigé
- ($E_1$) $ ⇔$ $-7x≤3$ $⇔$ $x≥{3}/{-7}$ (attention! $-7$<$0$)
Donc $\S_1=[-{3}/{7};+∞[$. - Le membre de gauche de ($E_2$) est un trinôme avec $a=1$, $b=2$ et $c=-7$.
$Δ=b^2-4ac=2^2-4×1×(-7)=32$.
$Δ>0$. Le trinôme a 2 racines
$x_1={-b-√Δ}/{2a}={-2-√{32}}/{2×1}=-1-2√{2}≈-3,8$
et $x_2={-b+√Δ}/{2a}={-2+√{32}}/{2×1}=-1+2√{2}≈1,8$.
D'où l'écriture factorisée:
$a(x-x_1)(x-x_2)=1(x-(-1-2√{2}))(x-(-1+2√{2}))=(x+1+2√{2})(x+1-2√{2})$
D'où le tableau de signes suivant:
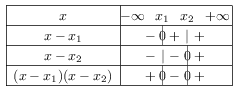
On recherche les x pour lesquels le produit est inférieur ou égal à 0.
Donc $\S_2=[-1-2√{2};-1+2√{2}]$
-
($E_3$) $ ⇔$ $(x-3)^2≤10$ $⇔$ $-√{10}≤x-3≤√{10}$
Soit: ($E_3$) $⇔$ $3-√{10}≤x≤3+√{10}$
Donc $\S_3=[3-√{10} ; 3+√{10}]$. - Le domaine d'étude est $\D_4=ℝ\\\{3\}$
Cela implique que 3 ne peut pas être une solution de cette inéquation.
($E_4$) $ ⇔$ ${1}/{x-3}≤2$ $⇔$ $x-3$<$0$ ou $x-3≥{1}/{2}$
Soit: ($E_4$) $⇔$ $x$<$3$ ou $x≥3+0,5$
Soit: ($E_4$) $⇔$ $x$<$3$ ou $x≥3,5$
Donc $\S_4=]-∞;3[∪[3,5;+∞[$. - Le domaine d'étude est $\D_5=[5;+∞[$
Cela implique que les réels strictement inférieurs à 5 ne peuvent pas être solution de cette inéquation.
($E_5$) $ ⇔$ $√{x-5}≤9$ $⇔$ $0≤x-5≤9^2$
Soit: ($E_5$) $⇔$ $0+5≤x≤81+5$
Soit: ($E_5$) $⇔$ $5≤x≤86$
Donc $\S_5=[5;86]$. -
($E_6$) $ ⇔$ $(x-1)^3≤8$ $⇔$ $(x-1)^3≤2^3$ $⇔$ $x-1≤2$
Soit: ($E_6$) $⇔$ $x≤3$
Donc $\S_6=]-∞;3]$.
A retenir
La résolution d'une inéquation se ramène généralement à la résolution d'une ou plusieurs inéquations de référence.
Savoir faire
Pour résoudre une inéquation, il suffit de transposer certains termes et de se ramener à la résolution d'une inéquation de référence.
Si la méthode ne fonctionne pas, il est conseillé de transposer le membre de droite pour obtenir une inéquation du type $f(x)≤0$ (ou $f(x)<0$ ou $f(x)≥0$ ou $f(x)>0$).
Factoriser $f(x)$, ou l'écrire sous forme d'un quotient permet souvent de conclure; en effet, le signe d'un produit ou d'un quotient est souvent facile à déterminer.
Exemple
Résoudre chacune des inéquations suivantes.
($E_1$) $3(x-1)^2≤5$
($E_2$) $x^3≤x^2$
($E_3$) $x^2≤{1}/{x}$
Corrigé
Soit: ($E_1$) $ ⇔$ $1-√{{5}/{3}}≤x≤1+√{{5}/{3}}$ $⇔$ ${3-√{15}}/{3}≤x≤{3+√{15}}/{3}$
$\S_1=[{3-√{15}}/{3};{3+√{15}}/{3}]$.
Déterminons le signe du produit.
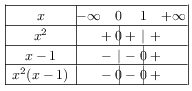
On recherche les x pour lesquels le produit est inférieur ou égal à 0.
Donc $\S_2=]-∞;1]$.
On retrouve les positions relatives de la signoïde représentant la fonction cube et de la parabole représentant la fonction carré.
Donc le domaine d'étude est $\D_3=ℝ\\\{0\}$.
($E_3$) $ ⇔$ $x^2-{1}/{x}≤0$ $ ⇔$ ${x^3}/{x}-{1}/{x}≤0$
Soit: ($E_3$) $ ⇔$ ${x^3-1}/{x}≤0$
Déterminons le signe du quotient.
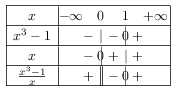
On recherche les x pour lesquels le quotient est inférieur ou égal à 0.
$\S_3=]0;1]$.
On retrouve les positions relatives de la parabole représentant la fonction carré et de l'hyperbole représentant la fonction inverse.