 Intégrales
Intégrales
A SAVOIR: le cours sur les intégrales
Exercice 7
Soit $f$ la fonction définie sur $ℝ$ par $f(x)=xe^{-x}$
et soit $C $ la courbe représentative de la fonction $f$ dans un repère du plan.
1.a. Déterminer la limite de $f$ en $-∞$ .
1.b. Déterminer la limite de $f$ en $+∞$.
1.c. En déduire les asymptotes éventuelles à la courbe $C $.
2.a. On note $f\,'$ la fonction dérivée de $f$ sur $ℝ$.
Démontrer que, pour tout $x$ de $ℝ$, on a: $f\,'(x)=e^{-x}(1-x)$.
2.b. Dresser le tableau de variations de $f$ sur $ℝ$.
3. Soit $g$ la fonction définie sur $ℝ$ par $g(x)=-(x+1)e^{-x}$.
Montrer que $g$ est une primitive de $f$ sur $ℝ$.
4. Etudier le signe de $f(x)$ sur $ℝ$.
5. On note $A$ l'aire (en unités d'aire) du domaine $D$ délimité par $C $, l'axe des abscisses, et les droites d'équations $x=0$ et $x=\ln 10$.
Déterminer la valeur exacte, puis une valeur arrondie au centième de $A$.
Corrigé
1.a. Tu peux cliquer ICI pour revoir quelques limites de référence.
On a: $\lim↙{x→-∞}-x=+∞$.
Or: $\lim↙{y→+∞}{e^y}=+∞$.
Donc: $\lim↙{x→-∞}e^{-x}=+∞$ (limite d'une composée).
Par ailleurs: $\lim↙{x→-∞}x=-∞$.
Donc, finalement: $\lim↙{x→-∞}xe^{-x}=-∞$ (limite d'un produit).
Soit: $\lim↙{x→-∞}f(x)=-∞$.
1.b. Tu peux cliquer ICI pour revoir les opérations sur les limites.
On sait que: $\lim↙{x→+∞}{e^x}/{x}=+∞$, et donc que: $\lim↙{x→+∞}{x}/{e^x}=0$.
Soit: $\lim↙{x→+∞}xe^{-x}=0$. Soit: $\lim↙{x→+∞}f(x)=0$.
1.c. D'après le 1.b., l'axe des abscisses est asymptote à la courbe $C $ en $+∞$.
2.a. Tu peux cliquer ICI pour revoir les opérations sur les dérivées.
On pose: $u=x$ et $v=e^{-x}$.
Oa a alors: $u\,'=1$ et $v\,'=(-1)e^{-x}=-e^{-x}$.
Ici: $f=uv$ et $f\,'=u\,'v+uv\,'$.
Donc: $f\,'(x)=1e^{-x}+x(-e^{-x})=e^{-x}(1-x)$.
Soit: $f\,'(x)=e^{-x}(1-x)$.
2.b. On note que $e^{-x}$ reste strictement positif pour tout réel $x$.
Par conséquent, $f\,'(x)$ est du signe de $1-x$ (fonction affine de c.d. négatif s'annulant en 1).
D'où le tableau de signes de $f\,'$ et de variations de $f$ ci-dessous:
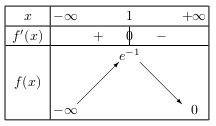
Notons que: $f(1)=e^{-1}$.
3. Tu peux cliquer ICI pour revoir le cours sur les primitives.
On pose: $u=-(x+1)=-x-1$ et $v=e^{-x}$.
Oa a alors: $u\,'=-1$ et $v\,'=(-1)e^{-x}=-e^{-x}$.
Ici: $g=uv$ et $g\,'=u\,'v+uv\,'$.
Donc: $g\,'(x)=-1e^{-x}+(-x-1)(-e^{-x})=e^{-x}(-1+x+1)=xe^{-x}=f(x)$.
Donc $g\,'=f$ sur $ℝ$.
Et par là, $g$ est bien une primitive de $f$ sur $ℝ$.
4. On note que $e^{-x}$ reste strictement positif pour tout réel $x$.
Par conséquent, $f\(x)$ est du signe de $x$.
Pour $x$<$0$, on a: $f(x)$<$0$.
Pour $x=0$, on a: $f(x)=0$.
Pour $x$>$0$, on a: $f(x)$>$0$.
5. Tu peux cliquer ICI pour revoir une propriété liant aires et intégrales.
La fonction $f$ est continue (car dérivable) sur $ℝ$ et positive sur $ℝ+$ (d'après le 4.).
Elle l'est donc en particulier sur $\[0;\ln10\]$.
Par conséquent:
$$A=∫_{0}^{\ln10} f(x)dx$$.
Soit: $A=\[g(x)\]_0^{\ln10}=g(\ln10)-g(0)=-(\ln10+1)e^{-\ln10}-(-(0+1)e^{-0})$.
Soit: $A=-(\ln10+1)(e^{\ln10})^{-1}+1=-(\ln10+1)(10)^{-1}+1=1-{\ln10+1}/{10}$.
Soit: $A={9-\ln10}/{10}$.
Et donc: $A≈0,67$ (unités d'aire).