 Intégrales
Intégrales
A SAVOIR: le cours sur les intégrales
Exercice 6
Soit $f$ la fonction définie sur l'intervalle $]0;+\∞[$ par $f(x)={1 + \ln x}/{x^2}$
et soit $C $ la courbe représentative de la fonction $f$ dans un repère du plan.
La courbe $C $ est donnée ci-dessous :
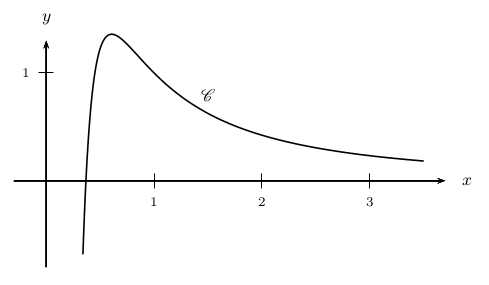
1.a. Déterminer la limite de $f$ en 0.
1.b. Que vaut $\lim↙{x→+∞}{\ln x}/{x}$. En déduire la limite de $f$ en $+∞$.
1.c. En déduire les asymptotes éventuelles à la courbe $C $.
2.a. On note $f\,'$ la fonction dérivée de $f$ sur l'intervalle $]0;+\∞[$.
Démontrer que, pour tout $x$ de $]0;+\∞[$, on a: $f\,'(x)={-1-2\ln x}/{x^3}$.
2.b. Résoudre sur l'intervalle $]0;+\∞[$ l'inéquation: $-1-2\ln x>0$.
2.c. Dresser le tableau de variations de $f$ sur l'intervalle $]0;+\∞[$.
3.a. Démontrer que $C $ admet un unique point d'intersection avec l'axe des abscisses. Préciser les coordonnées de ce point.
3.b. En déduire le signe de $f(x)$ sur l'intervalle $]0;+\∞[$.
4.a. Démontrer que la fonction $F$, définie sur l'intervalle $]0;+\∞[$ par $F(x)={-2- \ln x}/{x}$ est une primitive de la fonction $f$ sur l'intervalle $]0;+\∞[$.
4.b. Pour tout entier $n≥1$, on note $I_n$ l'aire (en unités d'aire) du domaine $D_n$ délimité par $C $, l'axe des abscisses, et les droites d'équations $x={1}/{e}$ et $x=n$.
Calculer $I_n$ en fonction de $n$.
4.c. Etudier la limite de la suite $(I_n)_{n∈ℕ}$.
Interpréter graphiquement le résultat obtenu.
Corrigé
1.a. Tu peux cliquer ICI pour revoir quelques limites de référence.
On note que: $f(x)=(1 + \ln x){1}/{x^2}$.
On a: $\lim↙{x→0}1=1$ et $\lim↙{x→0}\ln x=-∞$.
Donc: $\lim↙{x→0}1+\ln x=-∞$.
Par ailleurs: $\lim↙{x→0}{1}/{x^2}=+∞$.
Par conséquent, on obtient: $\lim↙{x→0}(1 + \ln x){1}/{x^2}=-∞$. (limite d'un produit)
Soit: $\lim↙{x→0}f(x)=-∞$.
1.b. Tu peux cliquer ICI pour revoir les opérations sur les limites.
On sait que: $\lim↙{x→+∞}{\ln x}/{x}=0$.
On fait apparaître ce terme dans l'expression de $f(x)$. On obtient: $f(x)=({1}/{x}+{\ln x}/{x}){1}/{x}$.
Or: $\lim↙{x→+∞}{1}/{x}=0$.
Par conséquent: $\lim↙{x→+∞}({1}/{x}+{\ln x}/{x}){1}/{x}=(0+0)×0=0$. Soit: $\lim↙{x→+∞}f(x)=0$.
1.c. D'après le 1.a., l'axe des ordonnées est asymptote à la courbe $C $.
D'après le 1.b., l'axe des abscisses est asymptote à la courbe $C $ en $+∞$.
2.a. Tu peux cliquer ICI pour revoir les opérations sur les dérivées.
On pose: $u=1+\ln x$ et $v=x^2$.
Oa a alors: $u\,'=0+{1}/{x}={1}/{x}$ et $v\,'=2x$.
Ici: $f={u}/{v}$ et $f\,'={u\,'v-uv\,'}/{v^2}$.
Donc: $f\,'(x)={{1}/{x}x ^2-(1+\ln x)2x}/{x^4}={x-2x-2x\ln x}/{x^4}={-x-2x\ln x}/{x^4}={x(-1-2\ln x)}/{x^4}={-1-2\ln x}/{x^3}$.
Soit: $f\,'(x)={-1-2\ln x}/{x^3}$.
2.b. Tu peux cliquer ICI pour revoir le cours sur la fonction ln.
On résout sur $]0;+\∞[$.
On a: $-1-2\ln x>0$ $⇔$ $-1>2\ln x$ $⇔$ $-0,5>\ln x$ $⇔$ $e^{-0,5}>e^{\ln x}$ $⇔$ $e^{-0,5}> x$.
Par conséquent: $S=]0;e^{-0,5}[$.
2.c. $f$ admet le tableau de variations suivant.
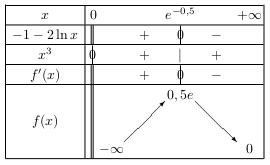
Notons que: $f(e^{-0,5})={1 + \ln e^{-0,5}}/{(e^{-0,5})^2}={1 -0,5 \ln e}/{e^{-1}}={1 -0,5 }/{e^{-1}}={0,5 }/{e^{-1}}=0,5e$.
3.a. On résout sur $]0;+\∞[$: $f(x)=0$ $⇔$ ${1 + \ln x}/{x^2}=0$ $⇔$ $1+\ln x=0$ $⇔$ $\ln x=-1$ $⇔$ $x=e^{-1}={1}/{e}$.
L'équation admet une solution et une seule. Donc $C $ admet un unique point d'intersection avec l'axe des abscisses.
Ce point a pour abscisse ${1}/{e}$.
Son ordonnée vaut évidemment $0$.
Pour les anxieux... Vérification: $f({1}/{e})={1 + \ln {1}/{e}}/{({1}/{e})^2}=(1-1)e^2=0$.
3.b. Finalement, d'après le 3.a. et le tableau de variation, on en déduit alors que $f$ est strictement négative sur $]0;{1}/{e}[$, et strictement positive sur $]{1}/{e}; +∞[$.
4.a. Tu peux cliquer ICI pour revoir le cours sur les primitives.
Montrons que $F\,'=f$ sur l'intervalle $]0;+\∞[$.
On pose: $u=-2- \ln x$ et $v=x$.
Oa a alors: $u\,'=0-{1}/{x}={-1}/{x}$ et $v\,'=1$.
Ici: $F={u}/{v}$ et $F\,'={u\,'v-uv\,'}/{v^2}$.
Donc: $F\,'(x)={{-1}/{x}x -(-2-\ln x)×1}/{x^2}={-1+2+\ln x}/{x^2}={1+\ln x}/{x^2}=f(x)$.
Donc la fonction $F$, définie sur l'intervalle $]0;+\∞[$ par $F(x)={-2- \ln x}/{x}$ est bien une primitive de la fonction $f$ sur l'intervalle $]0;+\∞[$.
4.b. Soit $n$ un entier tel que $n≥1$.
La fonction $f$ étant continue (car dérivable) et positive sur $\[{1}/{e};n\]$ (d'après le 3.b.), on en déduit que:
$$I_n=∫_{{1}/{e}}^n f(x)dx$$.
Donc: $I_n=F(n)-F({1}/{e})={-2- \ln n}/{n}-{-2- \ln ({1}/{e})}/{{1}/{e}}={-2- \ln n}/{n}-(-2-(-1))e={-2- \ln n}/{n}+e$.
Soit: $I_n={-2- \ln (n)}/{n}+e$.
4.c. On obtient facilement $\lim↙{n→+∞}-2- \ln n=-∞$ et $\lim↙{n→+∞}n=+∞$, ce qui conduit à une forme indéterminée.
On factorise alors le terme "dominant" du numérateur.
${-2- \ln n}/{n}={\ln n({-2}/{\ln n}- 1)}/{n}={\ln n}/{n}({-2}/{\ln n}- 1)$
Or: $\lim↙{n→+∞}\ln n=+∞$, et par là: $\lim↙{n→+∞}{-2}/{\ln n}- 1=0-1=-1$.
Or: $\lim↙{n→+∞}{\ln n}/{n}=0$.
Donc: $\lim↙{n→+∞}{\ln n}/{n}({-2}/{\ln n}- 1)=0×(-1)=0$.
Et finalement: $\lim↙{n→+∞} I_n=0+e=e$.
Autre méthode (qui fonctionne dans ce cas particulier):
On a: ${-2- \ln n}/{n}={-2}/{n}- {\ln n}/{n}$.
Comme: $\lim↙{n→+∞}{\ln n}/{n}=0$ et: $\lim↙{n→+∞}{-2}/{n}=0$, on obtient: $\lim↙{n→+∞} I_n=0+0+e=e$.
Quelle que soit la méthode, on a finalement: $\lim↙{n→+∞} I_n=e$.
On en déduit que l'aire du domaine $D_n$ tend vers $e$ lorsque $n$ tend vers $+∞$.
Le domaine $D_n$ est hachuré ci-dessous.
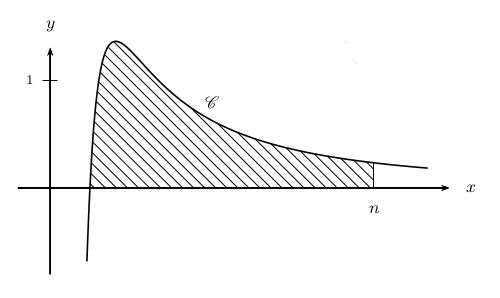
On notera que, comme $\lim↙{n→+∞} I_n=e$, l'aire du domaine "infini" délimité par $C $, l'axe des abscisses, et la droite d'équation $x={1}/{e}$ vaut $e$.
Nous sommes en présence d'un domaine de taille infinie qui possède une aire finie.